[一阶线性偏微分方程组的一般形式] 两个自变量的一阶线性方程组的形式是
![]()
或
(1)
其中Aij,Bij,Cij,Fi,aij,bij,fi是(x,t)的充分光滑函数.
[特征方程·特征方向·特征曲线]
![]()
称为方程组(1)的特征方程.在点(x,t)满足特征方程的方向![]() 称为该点的特征方向.如果一条曲线l,它上面的每一点的切线方向都和这点的特征方向一致,那末称曲线l为特征曲线.
称为该点的特征方向.如果一条曲线l,它上面的每一点的切线方向都和这点的特征方向一致,那末称曲线l为特征曲线.
[狭义双曲型方程与椭圆型方程] 如果区域D内的每一点都存在n个不同的实的特征方向,那末称方程组在D内为狭义双曲型的.
如果区域D内的每一点没有一个实的特征方向,那末称方程组在D内为椭圆型的.
[狭义双曲型方程组的柯西问题]
1° 化方程组为标准形式对角型
因为det(aij-ij)=0有n个不同的实根1(x,t) ![]() n(x,t),不妨设
n(x,t),不妨设
![]()
那末常微分方程
![]()
的积分曲线li (i=1,2,…,n)就是方程组(1)的特征曲线.
方程
![]()
的非零解(k(1) ![]() k(n))称为对应于特征方向k的特征矢量.
k(n))称为对应于特征方向k的特征矢量.
作变换
![]()
可将方程组化为标准形式对角型
![]()
所以狭义双曲型方程组可化为对角型,而一般的线性微分方程组(1)如在区域D内通过未知函数的实系数可逆线性变换可化为对角型的话,(此时不一定要求 i都不相同),就称这样的微分方程组在D内为双曲型的.
2° 对角型方程组的柯西问题
考虑对角型方程组的柯西问题
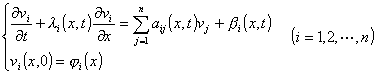
i(x)是[a,b]上的连续可微函数.设ij,i,i在区域D内连续可微,在D内可得相应的积分方程组
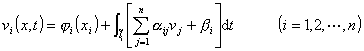
式中![]() 为第i条特征曲线li上点(x,t)与点(xi,0)之间的一段,(xi,0)为li与x轴上[a,b]的交点.上式可以更确切地写为
为第i条特征曲线li上点(x,t)与点(xi,0)之间的一段,(xi,0)为li与x轴上[a,b]的交点.上式可以更确切地写为
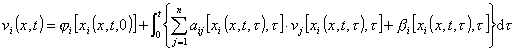
(i=1,2![]() n)
n)
式中xi=xi(x°,t°,t)为过点(x°,t°)的第i条特征曲线,利用逐次逼近法可解此积分方程.为此令
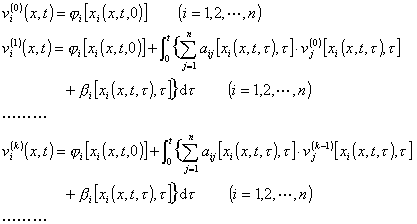
序列{vi(k)}(k=0,1,2![]() )一致收敛于积分方程的连续可微解vi(x,t) (i=1,2
)一致收敛于积分方程的连续可微解vi(x,t) (i=1,2![]() n),这个vi(x,t)也就是对角型方程组的柯西问题的解.
n),这个vi(x,t)也就是对角型方程组的柯西问题的解.
设在区域D内对角型方程组的柯西问题的解存在,那末解与初值有下面的关系:
(i) 依赖区间:过D中任意点M(x,t)作特征曲线l1,ln,交x轴于B,A,称区间[A,B]为M点的依赖区间(图14.1(a)),解在M点的值由区间[A,B]的初值确定而与[A,B]外的初值无关.
(ii)决定区域:过点A,B分别作特征曲线ln,l1,称ln,l1 与区间[A,B]围成的区域D1为区间[A,B]的决定区域(图14.1(b)),在区域D1中解的值完全由[A,B]上的初值决定.
(iii) 影响区域:过点A,B分别作特征曲线l1,ln,称l1,ln与[A,B]围成的区域D2为区间[A,B]的影响区域(图14.1(c)).特别当区间[A,B]缩为一点A时,A点的影响区域为D3(图14.1(d)).在区域D2中解的值受[A,B]上的初值影响,而在区域D2外的解的值则不受[A,B]上的初值影响.
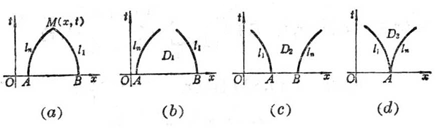
图14.1
[线性双曲型方程组的边值问题] 以下列线性方程组来说明:
(1)
1° 第一边值问题(广义柯西问题)
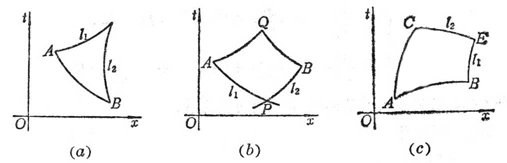
设在平面(x,t)上给定曲线段![]() ,它处处不与特征方向相切.过A,B分别引最左和最右的特征曲线l1及l2.要求函数u(x,t),v(x,t)在
,它处处不与特征方向相切.过A,B分别引最左和最右的特征曲线l1及l2.要求函数u(x,t),v(x,t)在![]() ,l1及l2围成的闭区域
,l1及l2围成的闭区域![]() 上满足方程组,且在
上满足方程组,且在![]() 上取给定的函数值(图14.2(a)).
上取给定的函数值(图14.2(a)).
2° 第二边值问题(古沙问题) 设l1是过P点的第一族特征线,l2是第二族特征线,在l1的一段PA上给定v(x,t)的数值,在l2的一段PB上给定u(x,t)的数值,过A点作第二族特征线,过B点作第一族特征线相交于Q.求在闭区域PAQB上方程组的解(图14.2(b)).
3° 第三边值问题 设AB为非特征曲线的曲线弧,AC为一特征线弧,且在AB与AC之间不存在过A点的另外特征曲线,过C点作第二族特征线与过B点的第一族特征线交于E点,在AC上给定v(x,t)的数值,在AB上给定u(x,t)的数值,求ACEBA所围成的闭区域D上的方程组的解(图14.2(c)).
|
图14.3 |
图14.2
[边值问题的近似解特征线法] 以上定解问题,可用逐步逼近法求解,也可用特征线法求解的近似值.以第一边值问题为例说明.
在曲线AB上取n个分点A1,A2,![]() An,并记A为A0,B为An+1,过A0按A0的第二特征方向作直线与过A1按A1的第一特征方向作直线相交于B0;过A1按A1第二特征方向作直线与过A2按A2的第一特征方向作直线相交于B1
An,并记A为A0,B为An+1,过A0按A0的第二特征方向作直线与过A1按A1的第一特征方向作直线相交于B0;过A1按A1第二特征方向作直线与过A2按A2的第一特征方向作直线相交于B1![]() 最后得到Bn(图14.3).用如下的近似公式来确定方程组(1)的解u(x,t),v(x,t)在Bi
(i=0,1,2,…,n)的数值:
最后得到Bn(图14.3).用如下的近似公式来确定方程组(1)的解u(x,t),v(x,t)在Bi
(i=0,1,2,…,n)的数值:
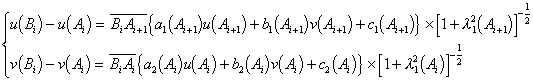
于是在一个三角形网格的节点上得到u,v的数值.再经过适当的插值,当n相当大,Ai、Ai+1的距离相当小时,就得到所提问题的足够近似的解.
[特殊形式的拟线性方程组可化约系统] 一般的拟线性方程组的问题比较复杂,目前研究的结果不多,下面介绍一类特殊形式的拟线性方程组可化约系统.如果方程组
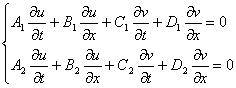
中所有的系数只是u,v的函数,称它为可化约系统.
考虑满足条件
![]()
的方程组的解u=u(x,t),v=v(x,t).x,t可以表示成u,v的函数,且
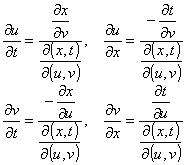
原方程化为
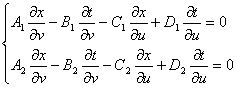
这是关于自变量u,v的线性方程组.这样就把求拟线性方程组满足![]() 的解,化为解线性方程组的问题.而此线性方程组满足条件
的解,化为解线性方程组的问题.而此线性方程组满足条件![]() 的解,在(x,t)平面上的象即为原来拟线性方程组的解.
的解,在(x,t)平面上的象即为原来拟线性方程组的解.