第四章 矩阵 · 行列式 · 线性方程组

本章内容包括矩阵、行列式与线性代数方程组两部分.

在前一部分，叙述了矩阵和行列式的基本概念，重点介绍各种类型矩阵的性质、基本运算，此外，还介绍了矩阵的特征值与特征矢量的求法，及有关的内容，如相似变换等；在线性方程组部分，着重介绍含n个未知量的n个方程的方程组解法，也简单地讨论了解的结构.最后对整系数线性方程组和线性不等式组也作了扼要说明.

                      §1  矩阵与行列式

一、矩阵及其秩

       [矩阵与方阵]  数域（第三章，§ 1）F上的m×n个数a_ij (i=1,2,…,m;j=1,2,…,n)按确定的位置排成的矩形阵列，称为m×n矩阵.记作

A=

其中横的一排叫做行，竖的一排叫做列，a_ij称为矩阵的第i行第j列的元素，矩阵A简记为(a_ij)或(a_ij)_m´n.

n×n矩阵也称为n阶方阵，a₁₁，a₁₂，…，a_nn称为矩阵A的主对角线的元素.

行数m与列数n都是有限的矩阵，称为有限矩阵.否则称为无限矩阵.

[矢量的线性相关与线性无关]对于n维空间的一组矢量x₁，x₂，…，x_m，若数域F中有一组不全为零的数k_i (i=1，2，…，m)，使

k₁x₁+k₂x₂+…+k_mx_m=0

成立，则称这组矢量在F上线性相关，否则称这组矢量在F上线性无关.

矢量组的线性相关性的讨论：

1°  矢量组x₁，x₂，…，x_m线性相关的充分必要条件是：其中至少有一个矢量x_i可用其他矢量的线性组合来表示，即

2°  包含零矢量的矢量组一定线性相关.

3°  矢量组x₁，x₂，…，x_m中，若有两个矢量相等：x_i=x_j(i≠j),则该矢量组线性相关.

4°  若矢量组x₁，x₂，…，x_r线性相关，则再添加若干个矢量后所组成的矢量组仍然线性相关；若矢量组x₁，x₂，…，x_m线性无关，则其中任一部分矢量组成的矢量组也线性无关.

5°  若x₁，x₂，…，x_r线性无关，而x₁，x₂，…，x_r+1线性相关，则x_r+1可以表示为x₁，x₂，…，x_r的线性组合.

[行矢量与列矢量 · 矩阵的秩]  由矩阵任一行的元素构成的n维矢量称为行矢量，记为

aⁱ=(a_i1,a_i2,...,a_in)        (i=1,2,...,m)

由矩阵任一列的元素构成的m维矢量称为列矢量，记为

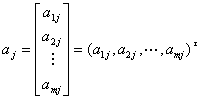         (j=1,2,...,n)

式中t表示转置，即行（列）转换为列（行）.

若矩阵A的n个列矢量中有r个线性无关（r≤n），而所有个数大于r的列矢量组都线性相关，则称数r为矩阵A的列秩.类似可定义矩阵A的行秩.

矩阵A的列秩与行秩一定相等，它也称为矩阵的秩，记作rank A=r.

矩阵的秩也等于该矩阵中不等于零的子式（见本节，二）的最大阶数.

二、行列式

    1. 行列式及其拉普拉斯展开定理

    [n阶行列式]  设

是由排成n阶方阵形式的n²个数a_ij(i,j=1,2,...,n)确定的一个数，其值为n！项之和

式中k₁,k₂,...,k_n是将序列1,2,...,n的元素次序交换k次所得到的一个序列，Σ号表示对k₁,k₂,...,k_n取遍1,2,...,n的一切排列求和，那末数D称为n阶方阵相应的行列式.例如，四阶行列式是4！个形为的项的和，而其中a₁₃a₂₁a₃₄a₄₂相应于k=3,即该项前端的符号应为

(－1)³.

若n阶方阵A=（a_ij）,则A相应的行列式D记作

D=|A|=detA=det(a_ij)

若矩阵A相应的行列式D=0，称A为奇异矩阵，否则称为非奇异矩阵.

       [标号集]  序列1,2,...,n中任取k个元素i₁,i₂,...,i_k满足

1≤i₁<i₂<...<i_k≤n                                                            (1)

i₁,i₂,...,i_k构成{1,2,...,n}的一个具有k个元素的子列，{1,2,...,n}的具有k个元素的满足(1)的子列的全体记作C(n,k),显然C(n,k)共有个子列.因此C(n,k)是一个具有个元素的标号集（参见第二十一章，§1，二），C(n,k)的元素记作σ,τ,..., σ∈C(n,k)表示

σ={i₁,i₂,...,i_k}

是{1,2,...,n}的满足(1)的一个子列.若令τ={j₁,j₂,...,j_k}∈C(n,k),则σ=τ表示i₁=j₁,i₂=j₂,...,i_k=j_k.

       [子式 · 主子式 · 余子式 ·代数余子式]

从n阶行列式D中任取k行与k列（1≤k≤n－1）,由这k行与k列交点处的元素构成的k阶行列式称为行列式D的k阶子式，记作

,     σ,τ∈C(n,k)

如果所选取的k行k列分别是第i₁,i₂,...,i_k行与第i₁,i₂,...,i_k列，则所得到的k阶子式称为主子式.即当σ=τ∈C(n,k)时，是主子式.

从行列式D中划去k行（σ）与k列（τ）后得到的n－k阶行列式称为子式的余子式，记作.

如果σ={ i₁,i₂,...,i_k}，τ={ j₁,j₂,...,j_k}，则称

为子式的代数余子式.

特别，当k=1时，σ={i}，τ={j},子式就是一个元素a_ij, a_ij的余子式记作，a_ij的代数余子式记作A_ij,即

且有 （2）

或 （3）

       [拉普拉斯展开定理]  在n阶行列式D中任取k行（1≤k≤n-1）,那末包含于所选定的这些行中的所有k阶子式与它们各自的代数余子式的乘积之和等于行列式D，即对任意σ∈C(n,k)，1≤k≤n-1，

（4）

式中∑表示对标号集C(n,k)中的所有元素求和.

拉普拉斯定理中是对行进行的，对列有类似结果

（5）

此外还有

（6）

（7）

显然（2），（3）分别是（6），（7）的特例.

[拉普拉斯恒等式]  设A=(a_ij)_m´n,B=(b_ij) _m´n(m≥n),又设l=,A的所有n阶子式为U₁，U₂，...，U_l，B的相应的n阶子式为V₁,V₂,...,V_l,则

det(A^τB)=

    2.行列式的性质

    1°  ïA₁A₂LA_mï=ïA₁ïïA₂ïLïA_mï

ïA^mï=ïAï^m,    ïkAï=kⁿïAï

式中A₁，A₂，L，A_m全为n阶方阵，k为任一复数.

    2°  行与列互换后，行列式的值不变，即

||=|A|

式中表示A的转置矩阵（见本章§2）.

    3° 互换行列式的任意两行（或列），行列式变号.例如

=

    4°  用数α乘行列式的一行（或列），等于将行列式乘以数α.例如

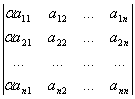=α

    5°  将行列式的一行（或列）元素乘以数α后加到另一行（或列）的相应元素上，行列式的值不变.例如

=

    6°  若行列式中有一行（或列）全为零，则行列式等于零.

若行列式中有两行（或列）对应的元素完全相同或成比例，则行列式为零.

若行列式中有一行（或列）元素是其他某些行（或列）对应元素的线性组合，则行列式为零.

    7°  若行列式中某一行（或列）的所有元素都可表示为两项之和，则该行列式可用两个同阶的行列式之和来表达.例如

=+

    3.几个特殊行列式

    [对角行列式]

=

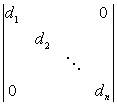[三角形行列式]

=

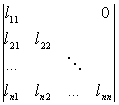    [二阶行列式]

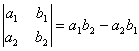
    [三阶行列式]

=++———

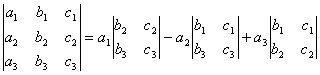
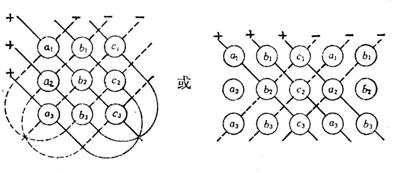记忆方法

行列式的值，等于各实线上元素乘积之和减去各虚线上元素乘积之和.

    [四阶行列式]

=-+-

         =-+

         +-+

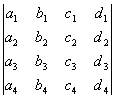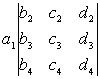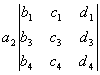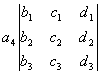
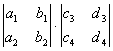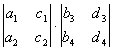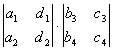
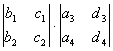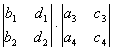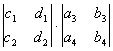
注意，四阶和四阶以上的行列式不能采用三阶行列式那种记忆方法，应按拉普拉斯展开定理采用逐步降阶的方法展开.

       [范德蒙行列式]

=

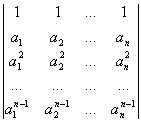式中Õ是对一切数对（i,j）（1£j<i£n）求积.

[倒数对称行列式]

=
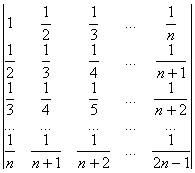