§3 仿射坐标系
一、 仿射坐标系与度量系数
[仿射坐标] 在三维欧氏空间*中,若取一个直角坐标系,其坐标单位矢量为i,j,k时,则空间中的矢量a可表示为
a=ax i+ay j+az k
一般地,在空间中给定了三个不共面的矢量e1,e2,e3,则空间中任一矢量a可按这三个矢量分解,令其系数为a1,a2,a3(这里1,2,3不是指数,而是上标)则a可表示为
a=a1e1+a2e2+a3e3
或简计作** a=aiei
a=![]() a1,a2,a3
a1,a2,a3![]() ={ ai}***
={ ai}***
这种坐标系![]() e1,e2,e3
e1,e2,e3![]() 称为仿射坐标系,e1,e2,e3称为坐标矢量,a1,a2,a3称为矢量a的仿射坐标.
称为仿射坐标系,e1,e2,e3称为坐标矢量,a1,a2,a3称为矢量a的仿射坐标.
[欧氏空间中度量系数] 当矢量a写成上面的形式时,则它的长度a由
(a)2=(aiei)(ajej)=(eiej)aiaj
给出.令
eiej=gij(=gji) (i,j=1,2,3)
则称gij为仿射坐标系的度量系数.
1![]() 矢量a的长度由
矢量a的长度由
(a)2=gijaiaj
计算.
2![]() 两个矢量
两个矢量
a=aiei,b=bjej
的夹角![]() 由
由
cos![]() =
=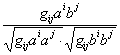
计算.
3![]() 因为gijaiaj是正定二次型,所以由gij所作的行列式
因为gijaiaj是正定二次型,所以由gij所作的行列式
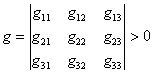
混合积
(e1,e2,e3)2= 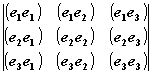 =g
=g
(e1,e2,e3)=![]()
[克罗内克尔符号] 对称矩阵
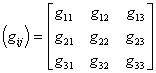
的逆矩阵用
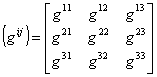
来表示.由逆矩阵的性质,有gij=gji和
gikgkj=![]()
式中
![]() =
=![]()
称为克罗内克尔符号.
[互易矢量] 利用这个gij规定
ei=gijej
因而有
ej=gijei
eiek=(gijej)ek=gij(ejek)=gijgjk=![]()
eiej=(gilel)(gjmem)=gilgjm(elem)=gilgjmglm=gil![]() =gij
=gij
对e1,e2,e3,可以得到
e1=![]() (e2×e3),
(e2×e3),
e2=![]() (e3×e1), e3=
(e3×e1), e3=![]() (e1×e2)
(e1×e2)
e1,e2,e3称为关于坐标矢量e1,e2,e3的互易矢量. gij称为互易矢量的仿射坐标系中的度量系数.