第二节 正态曲线下面积
直方图是以直方的面积表示数量的。直方顶端连成曲线后,整个曲线下面积就表示总频数,用1或100%表示。一定区间曲线下面积就是出现在此区间的频数与总频数之比,或出现在该区间的各个变量的概率之和。例如以7岁男童102人为100%,则若要知道坐高在66至68cm间的人数占总人数的百分比,只要知道曲线下横坐标为66至68cm区间内的面积就可以了。因此求出曲线下面积有其实用意义。
曲线下某区间的面积,可根据曲线方程用积分求得,但若每次应用时都要用积分计算,那是很麻烦的。前人已将标准正态曲线下0至各u值的面积计算出来的了。由于各书列的方式不完全相同,所以使用时要注意表上的图示或说明,仍用7岁男童坐高资料为例说明正态曲线下面积表(附表2)的使用方法。该表左侧及上端为u值,表中数字为横轴自0至u曲线下的面积。
例5.1 根据表4.3的资料计算得坐高的X=66.72,S=2.08,试估计总体中坐高在
(1)66.72-68.80cm间。
(2)66~68cm间及(3)68~70cm间的人数各占总人数的百分比。
(1)求坐高在66.72~68.80cm 之间曲线下面积。
①求u(u=(X-μ)/σ,这里分别以X、S作为μ与σ的估计值)
(66.72-66.72)/2.08=0
(66.80-66.72)/2.80=1
标准正态曲线下面积见图5.3(a)。
②查附表2,u自0至1的面积,即查u=1.00,得α/2=0.3413。坐高在此区间内的人数占总人数的34.13%。
(2)求坐高在66~68cm之间曲线下面积。
①求u
(66-66.72)/2.08=-0.346
(68-66.72)/2.08=0.615
标准正态曲线下面积见图5.3(b)
②查附表2 u=0.346,得α/2=0.1353(经内插法求得,下同)
u=0.615,得α/2=0.2308
0.1353+0.2308=0.3661
坐高在此区间内的人数占总人数的36.61%,即102×0.3661=37.3人,与实际观察所得38人相近。
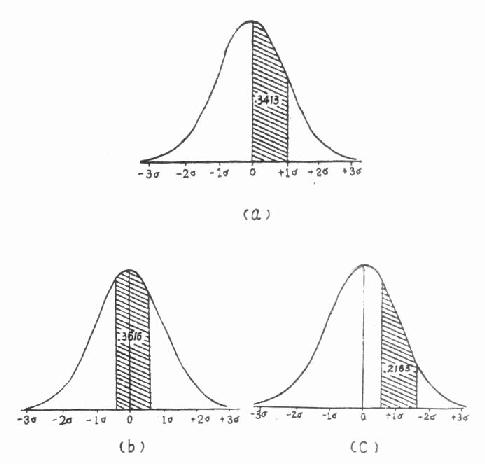
图5.3 正态曲线下面积之计算
(3)求坐高在68~70cm间的人数占总人数的百分比。
①求u
(68-66.72)/2.08=0.615
(70-66.72)/2.08=1.577
标准正态曲线下面积见图5.3(c)
②查附表2, u=1.577,得α/2=0.4426
u=0.615,得α/2=0.2308
0.4426-0.2308=0.2118
坐高在此区间内的人数点总人数的21.18%,即有102×0.2118=21.6人。与实际观察所得20人相近。
从例5.1可见,因为正态曲线对称于原点,所以不论u为正还是负,绝对值相同时,自0至u的面积相同。查附表2时,若两个u值中有一个是0,按另一u值查得α/2;若两个u异号,将查出的两个α/2值相加;若两个u同号,则将大的α/2值减去小的即得。但不能将两个u值相加(或减)后再查面积。
例5.1已求得u从0-1时,α/2=0.3413,所以u从-1~1,曲线下面积为0.6827,说明有68.27%的变量值在μ±σ的范围内(见图5.2)。查附表2,当u=1.96时,α/2=0.475,因此μ±1.96σ的范围内包含有95%的变量值,只有5%的变量值在此范围外。由于曲线左右对称,因此有2.5%的变量值等于或小于μ-1.96σ;2.5%变量值等于或大于μ+1.96σ。同理,查附表2,u=2.58时,α/2=0.495,因此μ±2.58σ范围内有99%的变量值,在此范围外的仅占1%。u=1.96和u=2.58(准确说是u=2.5758)是正态分布中两个重要的界值,称5%界和1%界,今后在正常值范围估计、假设检验等中常常要用到。
如果已知资料呈正态分布,那么理论上只要知道μ和σ就可根据曲线下面积表求出任两值之间变量值的个数,也就是说能算出变量值的频数分配。但实际上μ和σ常常无法获得,因此只能用X和S作为μ和σ的估计值,来估计总
体中变量值(个体值)的分布。
| 上一页:第一节 正态分布及其性质 |
| 当前页:第二节 正态曲线下面积 |
| 下一页:第三节 正常值范围的估计 |