三、确定正常值范围的方法
1.百分位数法。本法根据正常人样本数据,按照选定的百分范围计算相应的百分位数作为正常值范围的界值。可根据原始数据直接计算,亦可根据频数表进行计算。计算步骤为:
(1)按已确定的百分范围从表5.1查得应计算的百分位数;
(2)计算出各百分位数的所在位置;
(3)代入公式计算界限Px
表5.1 估计正常值范围的计算项目
| 百分范围(%) | 百分位数法 | 正态分布法 | ||
| 双侧 | 单侧 下(或上)限 | 双侧 | 单侧 下(或上)限 | |
| 80 | P10及P90 | P20(或P80) | X±1.282S | X-(或+)0.842S |
| 90 | P5及P95 | P10(或P90) | X±1.645S | X-(或+)1.282S |
| 95 | P 2.5及P97.5 | P5(或P95) | X±1.960S | X-(或+)1.645S |
| 98 | P1及P99 | P2(或P98) | X±2.326S | X-(或+)2.054S |
| 99 | P0.5及P99.5 | P1(或P99) | X±2.576S | X-(或+)2.326S |
例5.2 某地测得200例健康成人的血铅值(微克/100克)得频数分布如下,试估计单侧95%上限。
(1)查表5.1,百分范围95,百分位数法,单侧上限应求P95。
(2)求P95的位置200×0.95=190即为第190个数据处,因此知A=188,Lx=35,fx=4,ix=5。
代入公式(4.5)
表5.2 百分位数法计算单侧上限(200例健康成人的血铅值)
| 血铅值(微克/100克) | 频数 | 累计频数 |
| 0- | 6 | 6 |
| 5- | 48 | 54 |
| 10- | 43 | 97 |
| 15- | 36 | 133 |
| 20- | 28 | 161 |
| 25- | 13 | 174 |
| 30- | 14 | 188 |
| 35- | 4 | 192 |
| 40- | 4 | 196 |
| 45- | 1 | 197 |
| 50- | 2 | 199 |
| 55- | 0 | 199 |
| 60- | 1 | 200 |
| 合计 | 200 | - |
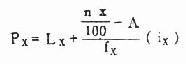
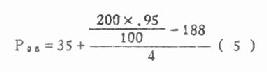
健康成人血铅值的95%正常值上限为37.5微克/100克。
若根据原始资料计算,已算得Px的位置为第190个数据后,将原始数据从大至小排,第10个数据的值即为Px。
此法的优点是不拘资料的分布类型,计算简便,样本含量较大,分布较稳定时结果稳定。但估计结果受样本极差的限制,受两侧尾部数据的影响较大,尤其是百分范围较大(如大于95%)。样本含量不够在时,结果不够稳定。
2.正态分布法。正态分布法运用正态曲线下面积与μ±μασ的关系来估计数值范围的。在图5.2中曾提到μ±1.96σ的范围内包含了曲线下总面积的95%,亦就是总例数的95%。在此范围外则有2.5%的例数其数据值大于μ±1.96σ,另2.5%小于μ-1.96σ。因此,就可用μ±1.96σ来估计双侧95%的正常值范围。同理可用μ与相应的μασ 估计所需百分范围,μ可从附表2查得。但在实际中μ与σ常常是不知道的,只能用它们的估计值X与S
来代替。估计正常值范围时常用的百分范围与相应的X±us见表5.1。用正态分布法估
计正常值范围的公式为
X±uαs (5.4)
例5.3 测得西安市7岁男童102人坐高,X=66.72,S=2.08,试用正态分布法估计
双侧95%正常值范围。
查表5.1,百分范围95,正态分布法双侧,应求X±1.96S。
代入公式(5.4)
66.72±1.96×2.08=(62.6432,70.7968)
西安市7岁男童坐高的95%正常值范围为62.6~70.08公分。
此法适用于正态分布资料,样本均数和标准差比较稳定者,其优点是结果稳定,受两端尾部数据影响较小,也不受样本数据极差的限制,缺点是只适用于正态分布资料。医学上不少资料呈偏态分布,但计算较繁。
| 上一页:二、确定正常值范围的一般原则和步骤 |
| 当前页:三、确定正常值范围的方法 |
| 下一页:练习题 |