一、正态性检验
有些统计方法只适用于正态分布或近似正态分布资料,如用均数和标准差描述资料的集中或离散情况,用正态分布法确定正常值范围及用t检验两均数间相差是否显着等,因此在用这些方法前,需考虑进行正态性检验。
正态分布的特征是对称和正态峰。分布对称时众数和均数密合,若均数-众数>0,称正偏态。因为有少数变量值很大,使曲线右侧尾部拖得很长,故又称右偏态;若均数-众数<0称负偏态。因为有少数变量值很小,使曲线左侧尾部拖得很长,故又称左偏态,见图7.1(a)。
正态曲线的峰度叫正态峰,见图7.1(b)中的虚线,离均数近的或很远的变量值都较正态峰的多的称尖峭峰,离均数近或很远变量值都较正态峰的少的称平阔峰。
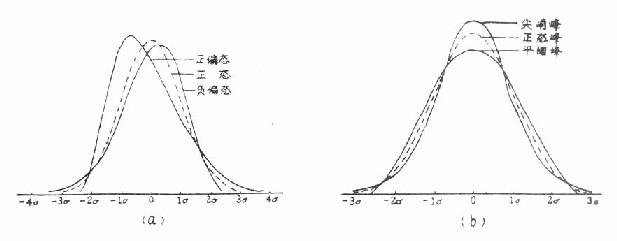
图7.1 频数分布的偏度和峰度
正态性检验的方法有两类。一类对偏度、峰度只用一个指标综合检验,另一类是对两者各用一个指标检验,前者有W法、D法、正态概率纸法等,后者有动差法亦称矩法。现仅将W法与动差法分述于下;
1.W法 此法宜用于小样本资料的正态性检验,尤其是n≤50时,检验步骤如下;
(1)将n个变量值Xi从小至大排队编秩。
X1<X2<……<XN<p
见表7.5第(1)栏,表中第(2)、第(3)栏是变量值,第(2)栏由上而下从小至大排列,第(3)栏由下而上从小至大排列。第(4)栏是第(3)栏与第(2)栏之差。
(2)由附表5按n查出ain系数列入表7.5第(5)栏,由于当n为奇数时,对应于中位数秩次的ain为0,所以中位数只列出,不参加计算。第(6)栏是第(5)栏与第(4)栏的乘积。
(3)按式(7.8)计算W值
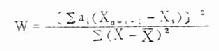
式中分子的∑,当n是偶数时,为 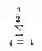
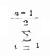 的缩写,表7.5
的缩写,表7.5第(6)栏的合计平方后即为分子。分母按原始资料计算。
(4)查附表6得P值,作出推断结论,按n查得W(n,α),α是检验前指定的检验水准,若W>W(n,α)则在α水准上按受H0,资料来自正态分布总体,或服从正态分布;若W≤W(n,α),则在α水准上拒绝H0,接受H1,资料非正态。
例7.8 测得20例40—49岁健康人右侧腓总神经的传导速度(m/sec)如表7.5第(2)、第(3)栏,试检验此资料是否服从正态分布。
H0:总体服从正态分布
H1:总体为非正态分布
α=0.05
计算表7.5各栏。
表7.5 W法正态性检验计算表
| 秩号 | 传导速度(m/sec) | ||||
| i (1) | Xi (2) | Xa-i+1 (3) | Xa-i+1-Xi (4)=(3)-(2) | ain (5) | ain(Xa-i+1-Xi) (6)=(5)(4) |
| 1 | 40.7 | 56.7 | 16.0 | 0.4734 | 7.5744 |
| 2 | 40.9 | 56.0 | 15.1 | 0.3211 | 4.8486 |
| 3 | 46.0 | 55.0 | 9.0 | 0.2565 | 2.3085 |
| 4 | 47.6 | 54.9 | 7.3 | 0.2085 | 1.5221 |
| 5 | 47.7 | 53.5 | 5.8 | 0.1686 | 0.9779 |
| 6 | 48.3 | 52.9 | 4.6 | 0.1334 | 0.6136 |
| 7 | 49.1 | 51.8 | 2.7 | 0.1013 | 0.2735 |
| 8 | 50.0 | 50.9 | 0.9 | 0.0711 | 0.0640 |
| 9 | 50.1 | 50.9 | 0.8 | 0.0422 | 0.0338 |
| 10 | 50.2 | 50.8 | 0.6 | 0.0140 | 0.0084 |
| 18.2240∑ain(Xa-i+1-Xi) | |||||
∑Xi=1004 ∑Xi2=50756.16 ∑(X-x)2=355.36
代入式(7.8)
W=(18.2240)2/355.36=0.9347
查附表6,n=20,α=0.05,W(20,0.05)=0.905
W>W(20,0.05) P>0.1,在α=0.05水准上接受H0,该资料服从正态分布。
2.动差法 又称矩法。既能用于小样本资料,亦可用于大样本资料的正态性检验。本法运用数学上三级动差和四组动差分别组成偏度系数与峰度系数,然后检验资料中否服从正态分布。当频数分布为正态时,偏度系数与峰度系数分别等于0,但从正态分布总体中抽出的随机样本,由于存在抽样误差,其样本偏度系数g1与样本峰度系数g2不一定为0,为此,需检验g1、g2与0的相差是否有显著性。其检验假设为①偏度系数等于O,即频数分布对称;②峰度系数等于0,即为正态峰。
偏度系数g1、峰度系数g2的公式见式(7.9)与(7.11)。当用频数表资料计算时可用式(7.10)与式(7.12),式中n为例数,f为频数。
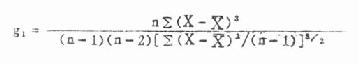
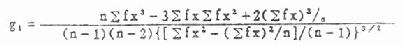
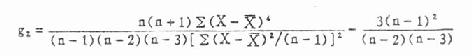
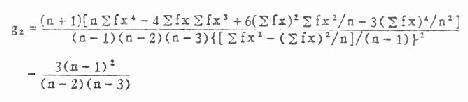
g1、g2的抽样误差分别为Sg1与Sg2,见式(7.13)与式(7.14)
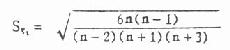
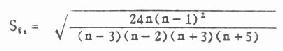
假设检验用u检验,其公式为
u1=g1/Sg1 (7.15)
u2=g2/Sg2 (7.16)
u的显著性界限为
∣u∣<1.96P>0.05在α=0.05的水准上接受H0。
1.96≤∣u∣<2.580.05≥P>0.01在α=0.05的水准上拒绝H0。
∣u∣≥2.58P≤0.01在α=0.01的水准上拒绝H0。
例7.9 用动差法检验例7.8的资料是否服从正态分布。
1.H0:频数分布对称,H1:频数分布不对称。
2.H0:频数分布为正态峰,H1:频数分布不是正态峰。
α=0.05
∑(X-x )2=355.36,∑(X-x )3=-1032.45
∑(X-x )4=20150.4316 n=20

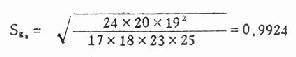
u2=0.6221/0.9924=0.627 P>0.20
在α=0.05的水准上接受H0,频数分布对称(P>0.05),并为正态峰(P>0.20)。因此可认为该资料服从正态分布。
| 上一页:第三节 正态性检验与两方差的齐性检验 |
| 当前页:一、正态性检验 |
| 下一页:二、两方差的齐性检验 |