三、直线回归方程的假设检验
(一)样本回归系数的假设检验
根据例9.1资料求得的是样本回归系数b,有抽样误差的,需作假设检验,检验其是否是从回归系数为0的假设总体(即β=0)中随机抽得的,也就是检验b与0的差别有无显着性。如果差别有显着性,可认为X与Y间有直线回归存在。
样本回归系数的假设检验亦用t检验。
H0:β=0即Y的变化与X无关;
H1:β≠0。
计算公式为:
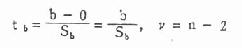
分母Sb是样本回归系数b的标准误,计算公式为:
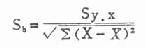
分子Sy.x为各观察值Y距回归线的标准差,即当X的影响被扣去以后Y方面的变异,可按下式计算:
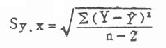
式中∑(Y-
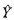
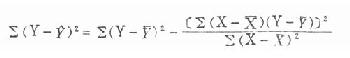
根据数理统计的理论,同一批资料计算所得tr与tb是相同的,即tr=tb。处理资料时可检验相关显著性代替其回归显著性。
由于例9.1资料的r在α=0.01水准上显著,故可判断样本回归系数-8.5045与0的相差有显著性,说明存在凝血时间随凝血酶浓度变化而变化的回归关系。
(二)两样本回归系数相差的假设检验
若有两个可以比较的样本,它们的回归系数分别为b1与b2,经检验都为显著,回归系数的标准误分别为Sb1和Sb2。b1与b2相差的显著性也可用t检验法检验,其计算公式为:
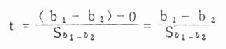
ν=n1+n2-4
式(9.11)中Sb1-b2为两样本回归系数之差的标准误,其计算公式为:
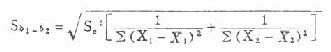
式(9.12)中S2C为两样本回归系数的合并方差,其计算公式为:
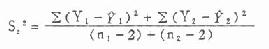
式(9.13)中∑(Y-
现以实例说明两样本回归系数t检验的步骤。
例9.2 表9.2资料为同一批白蛋白于38℃与25℃条件下,不同时间(分)的凝固百分比,问由此而得的两样本回归系数相差是否显著?
表9.2 白蛋白在两种温度下各不同时间的凝固百分比
| 时间(分) | 凝固百分比(%) | |
| X | Y1 | Y2 |
| 3 | 7.2 | 12.0 |
| 6 | 18.4 | 30.0 |
| 9 | 30.0 | 44.0 |
| 12 | 40.0 | 53.0 |
| 15 | 49.0 | 66.0 |
| 18 | 58.0 | 81.5 |
| 合计 63 | 202.6 | 286.5 |
本例图示见图9.10,本例计算见图下:
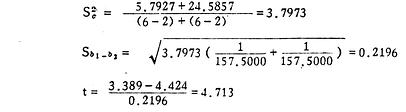
图9.10 白蛋白在两种温度下各不相同时间的凝固百分比
r1=0.998(P<0.01) b1=3.389∑(Y1-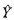
r2=0.996(P<0.01) b2=4.424∑(Y2-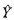
∑(X1-X1)2=∑(X2-X2)2=157.5000
1.H0:β1-β2=0
H1:β1-β2≠0
α=0.01
2.计算t值:
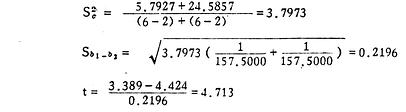
3.查t值表作结论:以ν=6+6-4=8查t值表,得
t0.01,8=2.355,今∣t∣>t0.01,8,故P<0.01。
4.判断结果:按α=0.01水准,拒绝H0,接受H1,故两个回归系数差别显著。说明两条回归直线的斜率不同,两条回归直线中X对Y的影响规律不一致。现b2>b1,说明随着时间的增加,蛋白质在38℃时凝固百分比的增加量比在25℃时高。
| 上一页:二、直线回归方程的计算法 |
| 当前页:三、直线回归方程的假设检验 |
| 下一页:第三节 计算相关与回归的注意事项 |