高中数学常用公式
一. 代数
1. 集合,函数

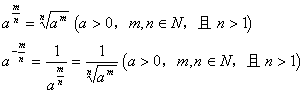
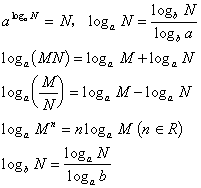
基本型:![]()
![]()
同底型:![]()
![]()
换元型:![]() 或
或![]()
2. 数列
(1)等差数列
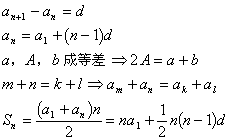
(2)等比数列
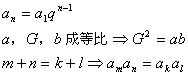
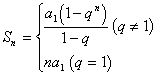
(3)求和公式
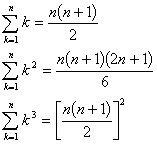
3. 不等式
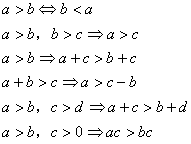
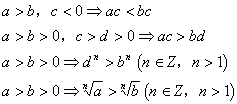
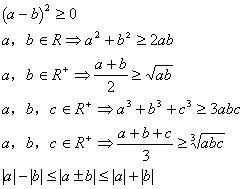
4. 复数
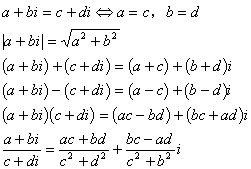
![]()
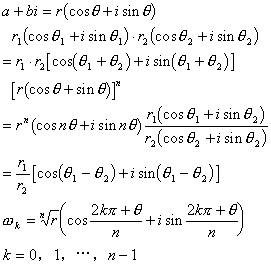
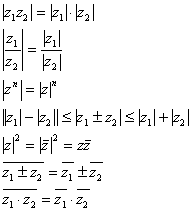
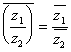
5. 排列组合与二项式定理
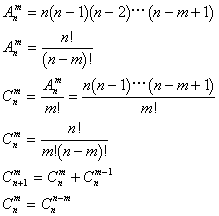
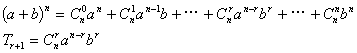
二. 三角函数
1. 同角关系
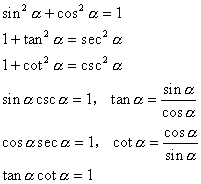
2. 诱导公式
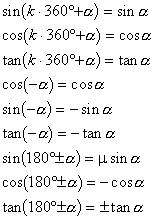
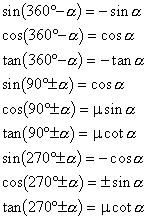
3. 和差公式
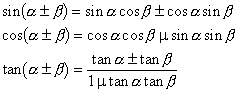
4. 倍角公式
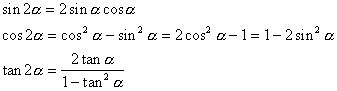
5. 半角公式
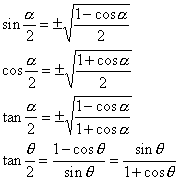
6. 万能公式
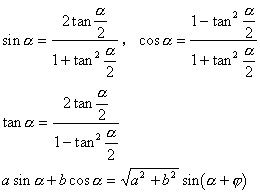
7. 正弦定理:
在一个三角形中,各边和它所对角的正弦的比相等,即:![]()
8. 余弦定理:
三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即:
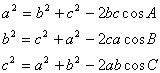
三. 向量运算
1. 向量的加法
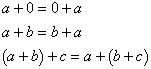
2. 向量减法
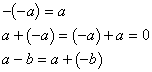
3. 实数与向量的积:以下公式![]() 为实数,
为实数,![]() 为向量
为向量
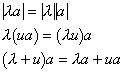
![]()
线段的定比分点:设![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,![]() ,则有:
,则有:
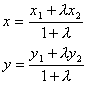
向量的数量积及运算律
数量积(内积):![]()
向量b在a方向的投影为![]()
设a、b都是非零向量,e是与b方向相同的单位向量,![]() 是a与e的夹角,则
是a与e的夹角,则
(1)![]()
(2)![]()
(3)当a与b同向时,![]() ;
;
当a与b反向时,![]() ;
;
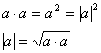
(4)![]()
(5)![]()
数量积运算律:(a,b,c为向量,![]() 为实数)
为实数)
![]() (交换律)
(交换律)
![]()
四. 解析几何
1. 直线方程
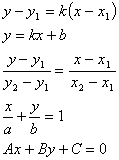
2. 两点距离、定比分点
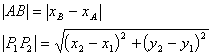
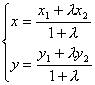
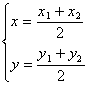
3. 两直线关系
![]()
或![]() 且
且![]()
![]() 与
与![]() 重合
重合![]()
或![]() 且
且![]()
![]() 与
与![]() 相交
相交![]()
或![]()
![]()
或![]()
![]() 到
到![]() 的角
的角
![]()
![]() 到
到![]() 的夹角
的夹角
![]()
点到直线的距离
![]()
4. 圆锥曲线
(1)圆
![]()
圆心为![]() ,半径为R
,半径为R
(2)椭圆
![]()
焦点![]()
![]()
离心率![]()
准线方程![]()
焦半径![]()
(3)双曲线:
![]()
(4)抛物线
抛物线![]()
焦点![]()
准线方程![]()
五. 立体几何
1. 空间两直线平行判定
(1)![]()
(2)![]()
(3)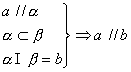
(4)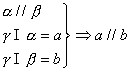
2. 空间两直线垂直判定
(1)![]()
(2)![]()
3. 直线与平面平行
(1)判定
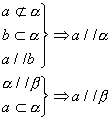
(2)性质
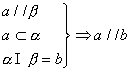
4. 直线与平面垂直
(1)判定
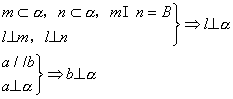
(2)性质
![]()
5. 平面与平面平行
(1)判定
![]()
(2)性质
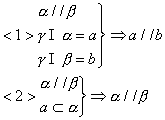
6. 平面与平面垂直
(1)判定
![]()
<2>二面角的平面角![]()
(2)性质
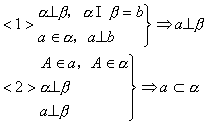
7. 几何体的侧面积
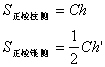
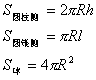
8. 几何体的体积
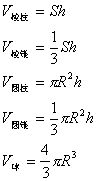
六. 概率与统计
1. 概率性质
(1)![]() ;
;
(2)![]()
2. 二次分布
![]()
3. 期望
![]()
若![]() ,则
,则![]()
4. 方差
![]()
5. 正态分布
![]()
式中的实数![]() 是参数,分别表示总体的平均数与标准差。
是参数,分别表示总体的平均数与标准差。
正态分布常记作![]()
标准正态分布,当![]() 时,
时,![]()
七. 极限
任何一个常数数列的极限都是这个常数本身。
即![]() (c是常数)
(c是常数)
![]()
极限四则运算
如果![]() ,那么
,那么
![]()
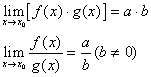
如果![]() ,那么
,那么
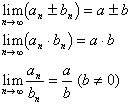
八. 导数
![]() (c为常数)
(c为常数)
![]()
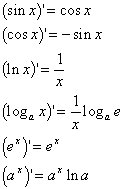
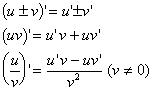
复合函数的导数![]()
九. 微分和积分
1. 微分:
![]() (其中
(其中![]() )
)
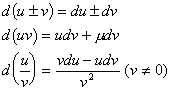
2. 不定积分:
![]() (c为常数)
(c为常数)
![]()
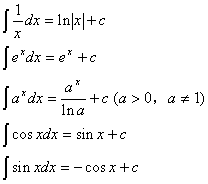
![]()
![]()
3. 定积分:
![]() (k为常数)
(k为常数)
![]()
![]() (其中
(其中![]() )
)
设![]() 在区间
在区间![]() 上的连续函数,
上的连续函数,![]() 是函数
是函数![]() 在区间
在区间![]() 上的任一原函数,即
上的任一原函数,即![]() ,则
,则
![]()