纵横图

    将从1至的自然数排列成纵横各有n个数的正方形．使每行、每列、有时还包括每条主对角线上的n个数的和都等于样的排列为n阶的纵横图，也称n阶幻方．中国历代数学著作中有许多关于纵横的记载，杨辉在《续古摘奇异法》（1275）卷一始有“纵横图”之名，其中给出了三至十阶的幻方及其变体共十三种．中国东汉末年郑立（129～～200年）注《易纬·乾凿度》：“太乙取其数以行九宫，四正四维皆合于十五”而得九宫数，即三阶幻方．（见图）

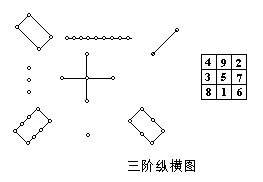
    共九个数从1至，每横行、纵行、对角线上三个数的和都等于

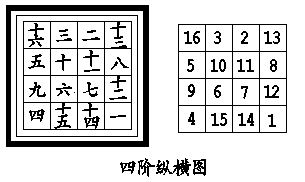
    清初，传教士传入《三三等数图》列三至十阶纵横图八种，并指出作图方法，英国人傅兰雅主编的《格致汇编》（1878）载有四阶纵横图（如图）欧洲研究纵横图造法开始于14世纪．

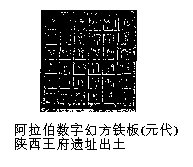
    元代安西王府旧址（今西安市郊），曾出土公元十五年（1278）阿拉伯学者扎马鲁丁为安西王推算历法期间所制作的“东阿拉伯系统”数码的铁制六阶幻方（1956年）出土．（如图）

    纵横图现在仍是组合数字研究的话题，广义幻方，幻体，双随机矩阵等都由它推广而来．