三角形的内角和
三角形内角和定理:三角形三个内角的和等于180°.
条件:△ABC
结论:∠A+∠B+∠C=180°
定理证明的其他方法(图示)

过A作DE∥BC

BC上任取一点D作DE∥BA,DF∥CA

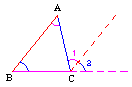
过C作CD∥BA

∠ACD=∠A+∠B
推论:三角形的一个外角等于和它不相邻的两个内角和.

∠ACD>∠A,∠ACD>∠B
推论:三角形的一个外角大于任何一个和它不相邻的内角.
三角形的内角和
三角形内角和定理:三角形三个内角的和等于180°.
条件:△ABC
结论:∠A+∠B+∠C=180°
定理证明的其他方法(图示)
过A作DE∥BC
BC上任取一点D作DE∥BA,DF∥CA
过C作CD∥BA
∠ACD=∠A+∠B
推论:三角形的一个外角等于和它不相邻的两个内角和.
∠ACD>∠A,∠ACD>∠B
推论:三角形的一个外角大于任何一个和它不相邻的内角.