隙积术是一类高阶等差数列求和的计算方法，这种求和法是我国宋代数学家沈括(1030～1093)首创．

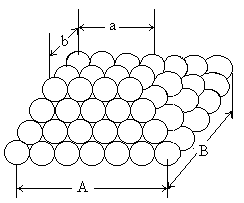
    如图所示，有n层圆球，各层都紧靠呈矩形，从下层到上层的长和宽上的球，依次各减少一个，设底层长有A个球，宽有B个球，顶层长有a个球，宽有b个球，问共有多少个球？

    设共有S个球，沈括的结论是：

    S=AB+(A-1)(B-1)+(A-2)(B-2)+……+(a+1)(b+1)+ab

    

    这是他的一个隙积术公式

    沈括以后，宋朝的杨辉在《详解九章算法》(1261年)和元朝的朱世杰在《四元玉鉴》(1303年)中又给出许多新的级数和公式，这些结果统称为垛积术．

    垛积术是隙积术成果的发展．