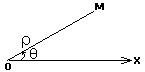
对于平面内任一点M,用ρ表示线段OM的长度,θ表示从Ox至OM的角度,ρ叫做点M的极径,θ叫做点M的极角,有序数对(ρ,θ)就叫做点M的极坐标,表示为M(ρ,θ)(如图).
平面内一点P与直角坐标是一一对应的,而与极坐标不能一一对应.一个极坐标只对应一个点,但一个点可以对应无数个极坐标.
![]()
极径也允许取负值.当ρ<0时,点M(ρ,θ)的位置按以下规则确定:
作射线OP,使∠xOP=θ,在OP的反向延长线上取一点M,使│OM│=│ρ│.点M就是坐标为(ρ,θ)的点.例如点M的极坐标既可表为
![]()
如果(ρ,θ)是一个点的极坐标,那么(ρ,θ+2kπ)、[-ρ,(2k+1)π]都可以作为它的极坐标(k∈Z).但如果限定ρ>0,0≤θ<2π或-π<θ≤π,那么除极点外,平面内的点和极坐标就可以一一对应了.当点M在极点时,它的极坐标ρ=0,θ可以取任意值.