)[对曲面面积的曲面积分]
1° 若S为逐片光滑的双侧曲面*
z=z(x,y) ((x,y))
式中σ为曲面S在Oxy坐标面上的投影，z(x,y)为单值连续可微函数，函数f(x,y,z)在曲面S的各点上有定义并连续，则
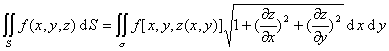
此积分与曲面S的方向（法线的方向）无关.
2° 若曲面S由连续可微函数
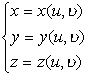((u,
)∈Ω)
给定，则
式中
* 曲面上某一点的法线方向的选定，唯一确定了曲面上所有其他点的法线方向，它们就是选定方向的
法线在曲面上连续移动（不经过曲面边缘）的指向，所以也就决定了曲面的一侧.如果改变原来选定
的法线方向，曲面上的所有其他点的法线方向都随着改变，曲面就从一侧移到另一侧.这种曲面称为
双侧曲面.
[对坐标的曲面积分] 若S为光滑的双侧曲面，
为它的正面，即由法线方向n(cosα, cosβ,cosγ)所确定的一侧，P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)为在曲面S上有定义并且连续的函数，则
若曲面S由连续可微函数
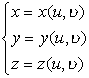((u,
)∈Ω)
给定，则
式中
[斯托克斯公式] 若C是包围逐片光滑有界双侧曲面S的逐段光滑简单闭曲线，P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)是在S+C上连续可微函数，则
[高斯公式] 若S为包含体积V的逐片光滑曲面P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)及其一阶偏导数在V+S上连续，则有高斯公式：
式中cosα,cosβ,cosγ为曲面S的法线正方向的方向余弦.