3、平方可积函数
[L2空间] 若S是有界可测集,f(x)为S上的可测函数,![]() 可积,并且
可积,并且
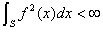
则称![]() 为属于空间
为属于空间![]() 的函数,记作
的函数,记作![]() ,或简写为
,或简写为![]() .
在本段中,假定S就是区间
.
在本段中,假定S就是区间![]() .
.
若![]() ,
,![]() ,则
,则![]() 都是可积的;并有
都是可积的;并有
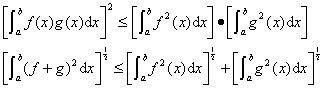
[模与距离] 设![]() ,则称
,则称
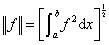
为f的模(范数).
设![]() 则称
则称
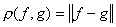
为f与g的距离.
设![]() 则
则
(i) ![]() ,只当
,只当![]() 几乎处处成立时,
几乎处处成立时,![]()
(ii) ![]()
(iii) ![]()
[平均收敛] 若![]() 并且
并且
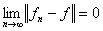
则称函数序列![]() 在
在![]() 内收敛或平均收敛,且其极限为
内收敛或平均收敛,且其极限为![]() ,记作
,记作
平均收敛有以下性质:
1o若![]() ,
,![]() 则
则
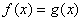
在![]() 上几乎处处成立.
上几乎处处成立.
2o若![]() ,
,![]() 则
则
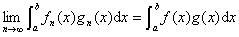
3o若![]() ,
,![]() 则
则
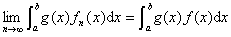
4o![]() 中点列
中点列![]() 平均收敛的充分必要条件是它为基本序列.
平均收敛的充分必要条件是它为基本序列.
基本序列的定义如下:设![]() ,若对任意
,若对任意![]() 总有正整数N,对一切
总有正整数N,对一切![]() ,使得
,使得
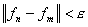
则称![]() 为
为![]() 中的基本序列.
中的基本序列.
由此可见![]() 是完备空间(见第二十一章,§4,一).
是完备空间(见第二十一章,§4,一).
[![]() 空间的可分性]
空间的可分性]
1o设![]() ,则对任意
,则对任意![]() ,总有连续函数
,总有连续函数![]() ,使
,使
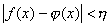
2o设![]() ,则对任意
,则对任意![]() ,总有系数为有理数的多项式
,总有系数为有理数的多项式![]() ,使
,使
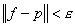
因为所有系数为有理数的多项式组成一个可数集合,并在![]() 中处处稠密. 所以2o表明
中处处稠密. 所以2o表明![]() 为可分空间(见二十一章,§3,三).
为可分空间(见二十一章,§3,三).