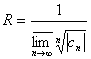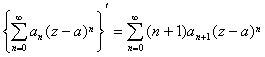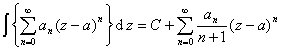§4  泰勒级数·罗朗级数·留数定理

一、泰勒级数与罗朗级数

   1.泰勒级数

   [泰勒级数展开定理] 设函数在圆（）内解析，那末在圆内可以展成泰勒级数

式中

其中是以为圆心，以（）为半径的圆周.这个展开式是唯一的.

    复变函数的泰勒级数展开式表与实变函数的幂级数展开式表（第五章§3，九）相类似，只要把实变量换成复变量就可以了.

    [复平面内的幂级数的收敛性] 如果幂级数

在圆内绝对收敛，而在圆外发散，那末称为级数的收敛圆，为收敛半径，并且

或者

   [阿贝耳定理] 对于每个幂级数

存在一个收敛半径（）具有下列性质：

    1^o  对于内每点，级数绝对收敛.在每一闭圆（）上，级数一致收敛.

    2^o  ,级数发散.

    3^o  在内，级数的和是一解析函数.

    由性质3^o和泰勒级数展开定理可知，复变函数在一点解析和在点的邻域内可以展开为幂级数是等价的.

   [运算规则] 在公共的收敛圆内，有下列运算规则：

                                        （）

                                         （是任意复数）