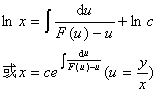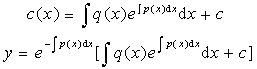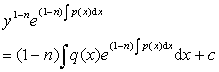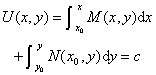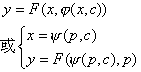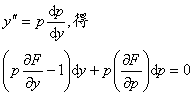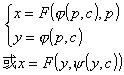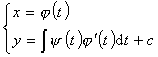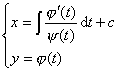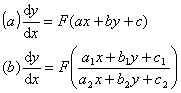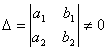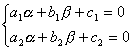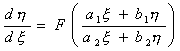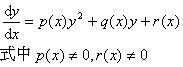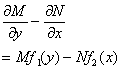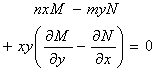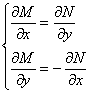二、可积类型及其通解
(表中c为任意常数)
|
方 程 类 型 |
解法要点与通解表达式 |
|
1.变量可分离方程 f1(x)g1(y)dx+ f2(x)g2(y)dy=0 |
分离变量,两边同除以g1(y)f2(x),再分别积分.
|
|
2. 齐次方程
一般假设 则变量可分离,属类型1 |
令 代入原方程,得新未知函数u关于自变量x的方程: xdu = [F(u) – u]dx 再按类型1求解.
|
|
3.线性方程
当q(x)
≡ 0, 称为齐次线性方程,当 |
先求出所对应的齐次线性方程 的通解 再利用常数变易法(本章§3,二,2),令
算出
|
|
4.伯努利方程
|
利用变量替换
|
|
5.全(恰当)微分方程 M(x,y)dx+N(x,y)dy=0 式中M,N满足
|
方程可写成 M(x,y)dx+N(x,y)dy=dU(x,y)=0 式中dU是全(恰当)微分.
|
|
6.可将y解出的方程 y=F(x,p) 式中 |
把方程两边对x求导数,得
或 如果能求出此方程的通解
|
|
[拉格朗日方程] y = xf1(p) + f2(p) 式中 [克莱罗方程] y = xp+F(p) 式中 |
可化为x的线性方程
再按类型3求解 化为方程
令
(见§2,三) |
|
7.可将x解出的方程 x = F(y, p) 式中 |
方程两边对x求导数,利用
如果可求出这个方程的通解 那末原方程可解.
|
|
8.不显含未知函数的方程 |
引入适当参数t,化原方程为
|
|
9.不显含自变量的方程 |
引入参数t,化原方程为
|
|
10.能化为变量可分离或齐次方程的方程
|
(a)令z = ax + by + c,化原方程为类型1
(b)若行列式
引进新变量
式中α,β满足方程组
则原方程化成齐次方程(类型2):
若 若 于是原方程化为类型1. |
|
11.黎卡提方程
|
如果已知原方程有一个特解y=y1(x), 作变换
可把原方程化为线性方程(类型3):
或用变换y = y1(x) + u 化为伯努利方程(类型4):
再分别按类型3和类型4求解. |
|
12. 含积分因子的方程 M (x, y) dx + N(x, y) dy = 0 式中
但存在μ(x, y)满足
μ(x, y)称为原方程的积分因子 |
找出积分因子μ(x, y),再按类型5求解.找积分因子的方法见下表. |
找积分因子的方法
|
条 件 |
积分因子 μ(x, y) |
条 件 |
积分因子 μ(x, y) |
|
xM+yN=0
xM+yN≠0 M,N是同次的齐次式
M(x, y) = yM1 (xy) N(x, y) = xN1(xy)
|
|
存在适合
即M+iN在使微分方程满足的单连通区域内是x+iy的解析函数 |
形为 m(x)n(y)
xmyn
|