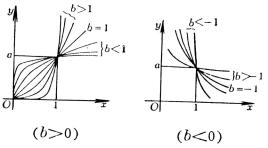
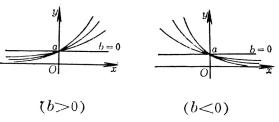
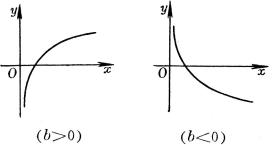
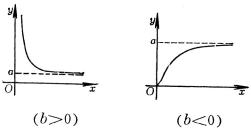
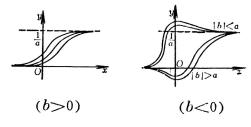
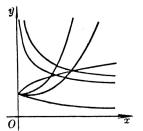
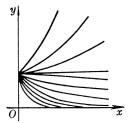
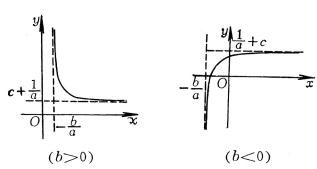
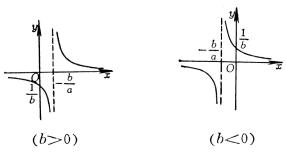
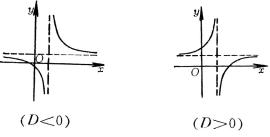
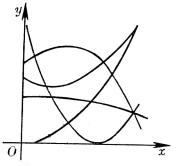
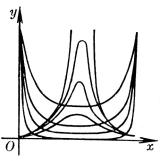
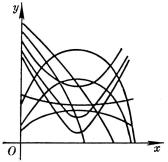
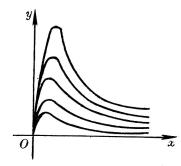
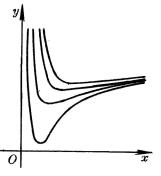
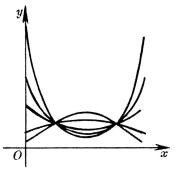
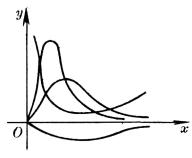
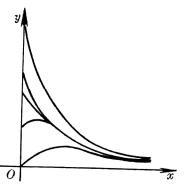
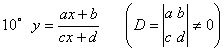4、可化成线性回归的曲线回归
如果观测数对在坐标纸上的分布形成曲线，可作适当的变量替换，对两个新的变量作线性回归。然后再还原到原来的变量。
可化直线型的常用曲线类型
|
曲 线 类 型 |
化直线型的变量替换 |
|
|
1°
|
设 则 (x, y)在双对数坐标纸上成一直线 |
|
|
|
设X = x , Y = 则 (x, y)在单对数坐标纸上成一直线 |
|
|
|
设 则 (x, y)在单对数坐标纸上成一直线 |
|
|
|
设 则 |
|
|
|
设 则 |
|
|
|
曲线与类型
|
c确定后，设 则 |
|
曲 线 |
类 型 |
化直线型的变量替换 |
|
|
曲线与类型 则 |
确定后，设 则 |
|
|
设 则 |
|
|
|
设 则 |
|
|
|
在曲线上取一点(x0 , y0) 设X = x 则 用回归直线法，从已给数据可定出A和B |
|
|
|
在曲线上取一点(x0 , y0) 设X = x 则 |
|
|
曲 线 类 型 |
化直线型的变量替换 |
|
|
|
设X = x 则可化为类型11° |
|
|
|
设X = x Y = y2 则可化为类型11° |
|
|
|
设X = x 则可化为类型11° |
|
|
|
设 则可化为类型11° |
|
|
|
设X = x 则
化为类型11° |
|
|
|
若给定的x值构成以h为公差的等差级数，则设
（取值
（取值 而得直线型 |
|
|
|
若给定的x值构成以h为公差的等差级数，设u1= x+h , u2= x+2h，其对应的y值为v1 ,v2 又设 而得
由此用回归直线法定出 b , d后，再设 则得 |
|
相同，只是在
轴方向上作了移动，首先在给定的曲线上取三点：
,
,
),则
相同，只是在
轴方向上作了移动，首先在给定的曲线上取三点：
