三、平稳随机过程
[弱平稳过程] 如果随机过程{x (t),tÎT}满足
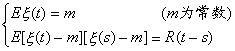
就称它是弱平稳过程(或广义的平稳过程)。
广义的平稳过程不一定是狭义的平稳过程;反过来,狭义的平稳过程也不一定是广义的平稳过程,但是如果狭义平稳过程的二阶矩存在,那末它必是广义的平稳过程。
对于正态过程来说,广义平稳性和狭义平稳性是一致的。
在理论研究中,考虑复值随机过程常常更加方便。所谓复值随机变量x是指x =η+ix ,其中η, x 都是随机变量;而复值随机过程就是x (t)=η(t)+ ix (t),其中η(t), x (t)都是实值随机过程。
复值随机变量x =η+ix 的均值(或数学期望)定义为
![]()
两个复值随机变量x 1,x 2的相关矩定义为
![]()
复值随机过程{x (t),tÎT}的广义平稳性,是指它满足
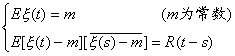
下面考虑的都是复值的广义平稳过程。
[相关函数的谱分解] 如果函数R(τ)是某一均方连续平稳过程{x (t), ![]() <t<
<t<![]() }的相关函数,那末
}的相关函数,那末
![]()
其中F(λ)是有界不减函数,满足![]() ,称为平稳过程{x (t),
,称为平稳过程{x (t),![]() <t<
<t<![]() }的谱函数(工程上称为频谱)。
}的谱函数(工程上称为频谱)。
如果F(λ)绝对连续,记![]() ,称
,称![]() 为谱密度(工程上称为频谱密度),这时
为谱密度(工程上称为频谱密度),这时
![]()
当{x (t), ![]() <t<
<t<![]() }是实值平稳过程时,相关函数R(τ)可以表示成
}是实值平稳过程时,相关函数R(τ)可以表示成
![]()
或(当谱密度存在时)
![]()
其中F1(λ)=2F(λ)+c(c为常数),![]() 。
。
特别,对复值平稳序列{x n, n=0,±1,L}有
![]() (k=0,±1,L)
(k=0,±1,L)
其中谱函数F(λ)满足
F(![]() )=0,
F(p)=R(0)
)=0,
F(p)=R(0)
[遍历性定理]
1° 如果{x (t),-∞<t<∞}是均方连续的平稳过程,那末
![]()
的充分必要条件是:
![]()
2° 如果{x n, n=0,±1,L}是平稳序列,那末
![]()
的充分必要条件是:
![]()
3° 如果{x (t),-∞<t<∞}是均值为零的均方连续的平稳过程,又对取定的常数 t >0,![]() 也是均方连续的平稳过程,记其相关函数为Rt (u),那末
也是均方连续的平稳过程,记其相关函数为Rt (u),那末
![]()
![]()
的充分必要条件是:
![]()
4° 如果{![]() n=0,±1,L}是均值为零的平稳序列,又对取定的整数m,
n=0,±1,L}是均值为零的平稳序列,又对取定的整数m, ![]() n=0,±1,L}也是平稳序列,记其相关函数为Rm(k),那末
n=0,±1,L}也是平稳序列,记其相关函数为Rm(k),那末
![]()
的充分必要条件是:
![]()
遍历性定理表明,对于平稳过程,只要它满足定理的条件(在实际中它们是常常能够满足的),那末对样本空间的平均(如均值、相关矩等)可以用对时间的平均来代替,更具体地说,只要用平稳过程在足够长时间的一次实现,就可以确定过程的均值和相关函数。这正是遍历性定理在实用上重要的原因。
[平稳过程的谱展式] 如果{x (t),-∞<t<∞}是均值为零的均方连续平稳过程,那末有
![]()
其中
![]()
满足 (i)EZ(l)=0
(ii)当区间![]() 与
与![]() 不相重叠时
不相重叠时
![]()
(即Z(l )是具正交增量的过程)
(iii)![]() (F(l )是谱函数)
(F(l )是谱函数)
Z(l )称为x (t)的随机谱函数,x (t)的积分表示式称为x (t)的谱展式。
特别,如果x (t)是实值均方连续平稳过程,那末有
![]()
其中
![]()
![]()
满足 (i)EZ1(l )=EZ2(l )=0,
(ii)当区间![]() 与
与![]() 不相重叠时
不相重叠时
![]() (j,k=1,2)
(j,k=1,2)
(iii)![]()
(F(l )是谱函数)
如果{x n, n=0,±1,L}是均值为零的平稳序列,那末有
![]()
其中随机谱函数Z(l )是
![]() (-p ≤λ≤p)
(-p ≤λ≤p)
它也满足类似于均方连续平稳过程的随机谱函数的性质(i)~(iii)。