+ + + =

分数阶微积分 Fractional Calculus

分数阶导数简介

二次半微分 = 1阶微分, `d^0.5/dx^0.5 d^0.5/dx^0.5 x = d/dx x = 1` 对于任意的o(x),由于伽玛函数的参数在实数部为负整数时没有定义，需要在分数微分前先进行整数微分。例如 `D^(3/2)`f(x)=`D^(1/2)D^1`f(x)=`d^(1/2)/dx^(1/2) d/dx` f(x) 这苻合Caputo的定义，Caputo的定义是先微分后积分，对于分数阶微分方程的初值要求与普通微分方程相同，因此本文釆用广义Caputo的定义: 积分下限a为f(x)的反函数`f^(-1)(0)` .

负阶导数 负阶导数相当积分, 负一阶等于积分, 负2阶是二重积分，负1/2阶是半积分. `d^(-0.5)/dx^(-0.5)` f(x) = `int f(x) (dx)^0.5`

复数阶微积分 以上微分算子的扩展不仅仅局限于实数阶。举个例子， (1-i)阶导数作用后， (1+i)阶导数再作用，可以得到二阶导数。 (1+i)阶微分和(1-i)阶微分 = 2阶微分, `d^(1+i)/dx^(1+i) d^(1-i)/dx^(1-i) sin(x) = d^2/dx^2 sin(x) = -sin(x)`

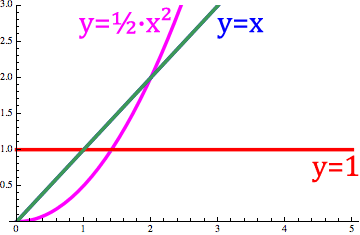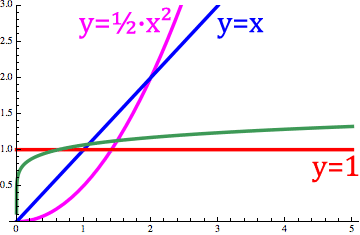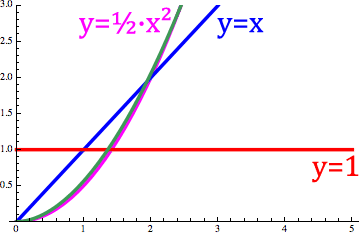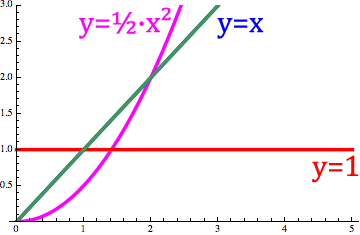
	可变阶微积分 Variable Order calculus 当阶数o(x)是变量时, 它是可变阶导数微分。 `d^cos(x)/dx^cos(x)` sin(x) = d(sin(x),x,cos(x)) 这个动画展示了不同分数微分算子D如何操作在 y=x（o(x)=0阶, 蓝色），结果（分数阶, 绿色）在一般的积分（o(x)= -1阶, y=x^2/2 ，紫色）及一般的一次微分（ o(x)=1阶, y=1 ，红色）间连续变化。
分数阶微分方程 Fractional differential equation `d^(pi)/dx^(pi)` y - y - 2exp(x) = 0	分数维空间 我们生活在的三维立体空间可以扩展到分数维空间，分数维空间对应分数阶导数, 分数阶导数的几何意义是分数维理论, 分数维理论就是分形理论.

计算

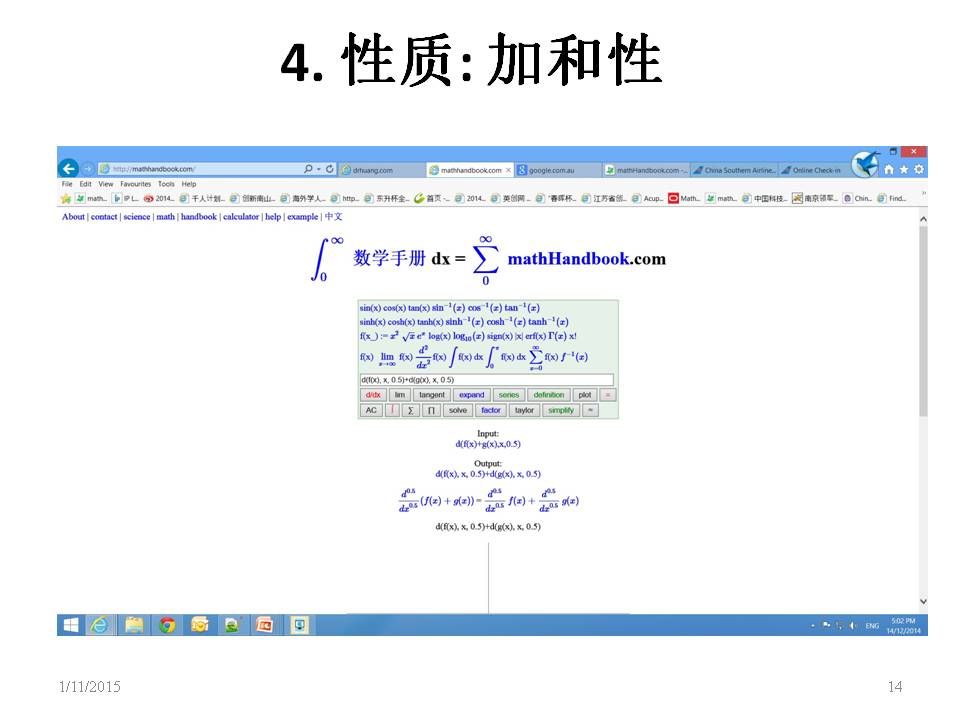
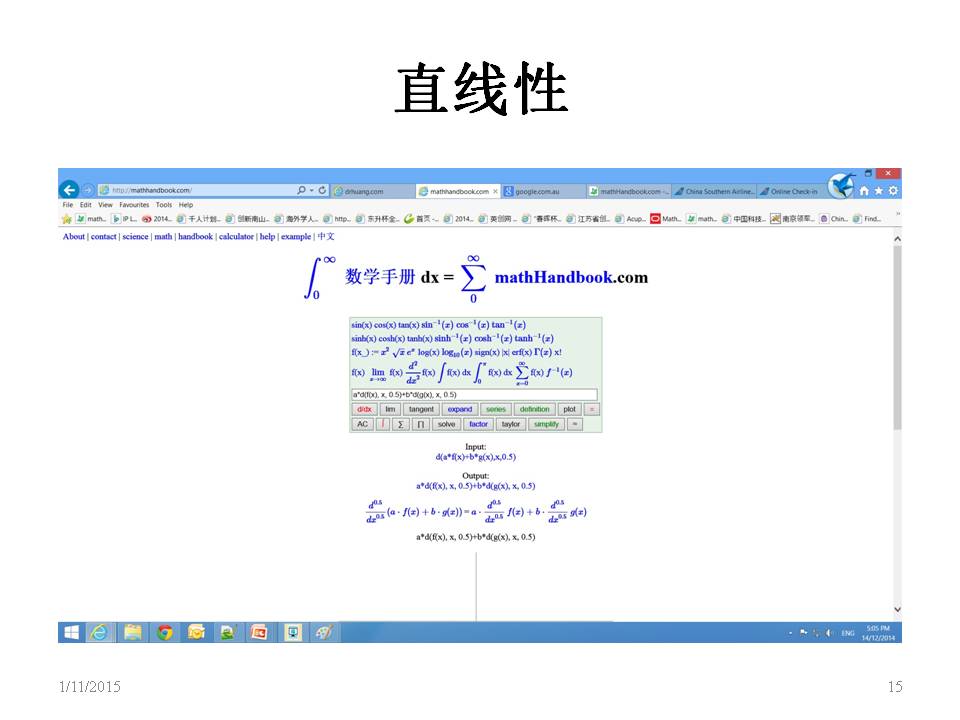
数学手册计算器是三合一 = 数学手册 + 计算器 + 计算机代数系统. 具有机器学习的功能，举一反三，解任意阶(0.5i 阶)微分方程的功能,世上独一无二。在数学手册网上输入数学公式，连续点击计算微积分，解方程，给出数值解，分析解和图解, 制图互动放大。随时随地学习，随时随地计算，随时随地开发。学习数学的好助手。 mathHand.com http://chinese.mathhandbook.com

使用经验

1. 怎么求函数的分数阶导数？兼谈数学手册计算器_百度经验
2. 分数阶导数 - qq_34040902的博客 - CSDN博客
3. 特殊的微分方程的解法_百度经验

例题

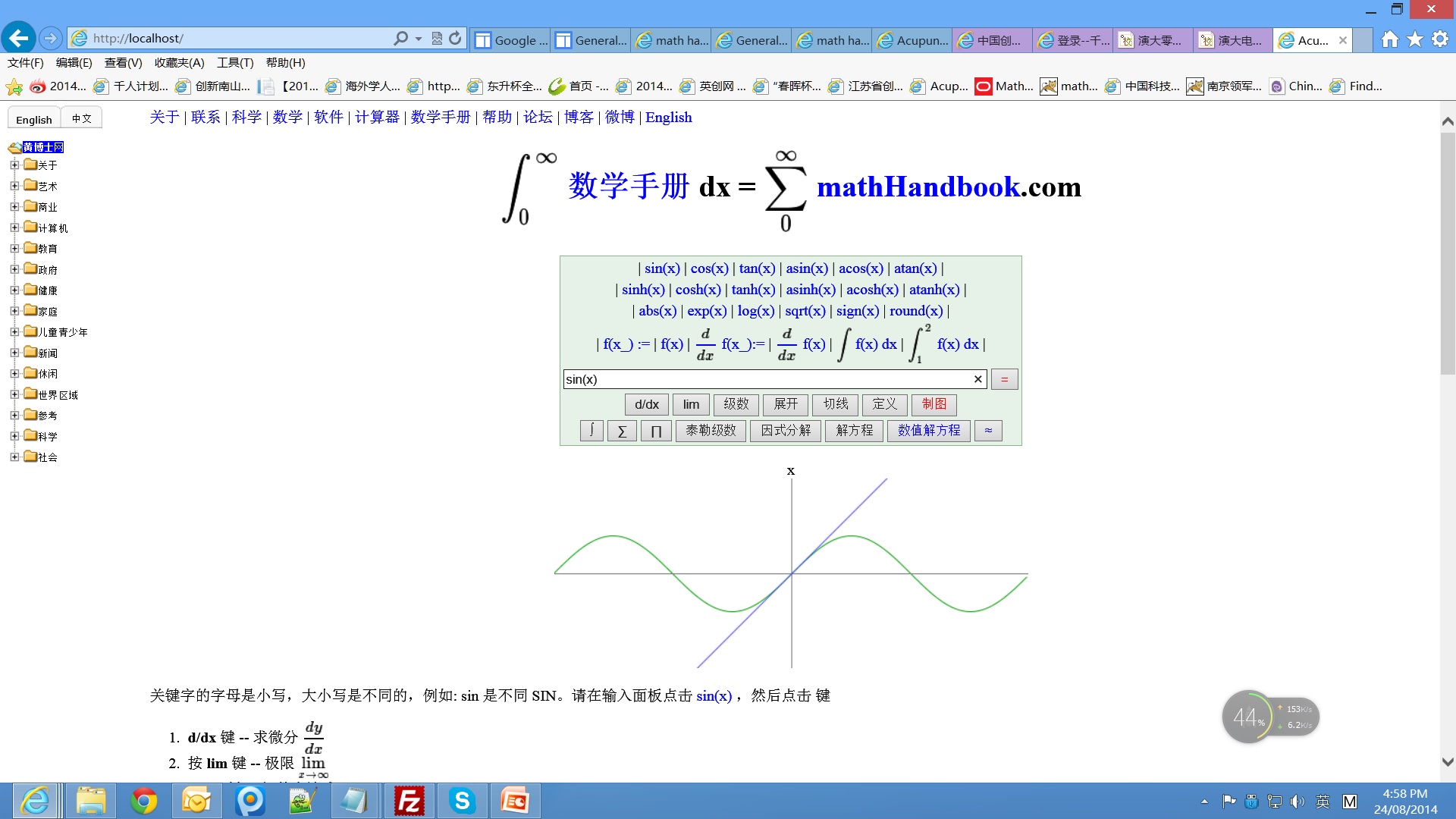
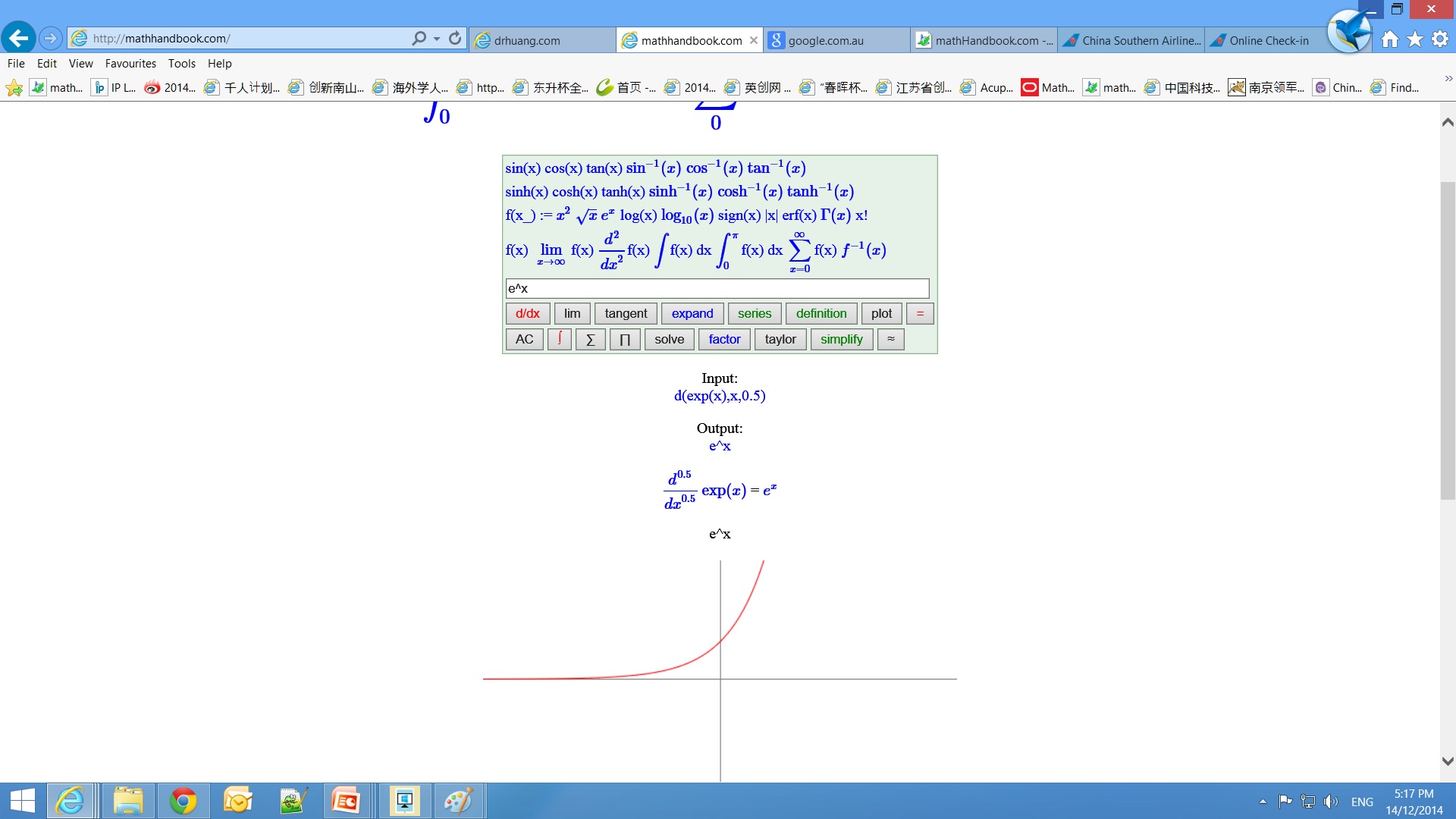
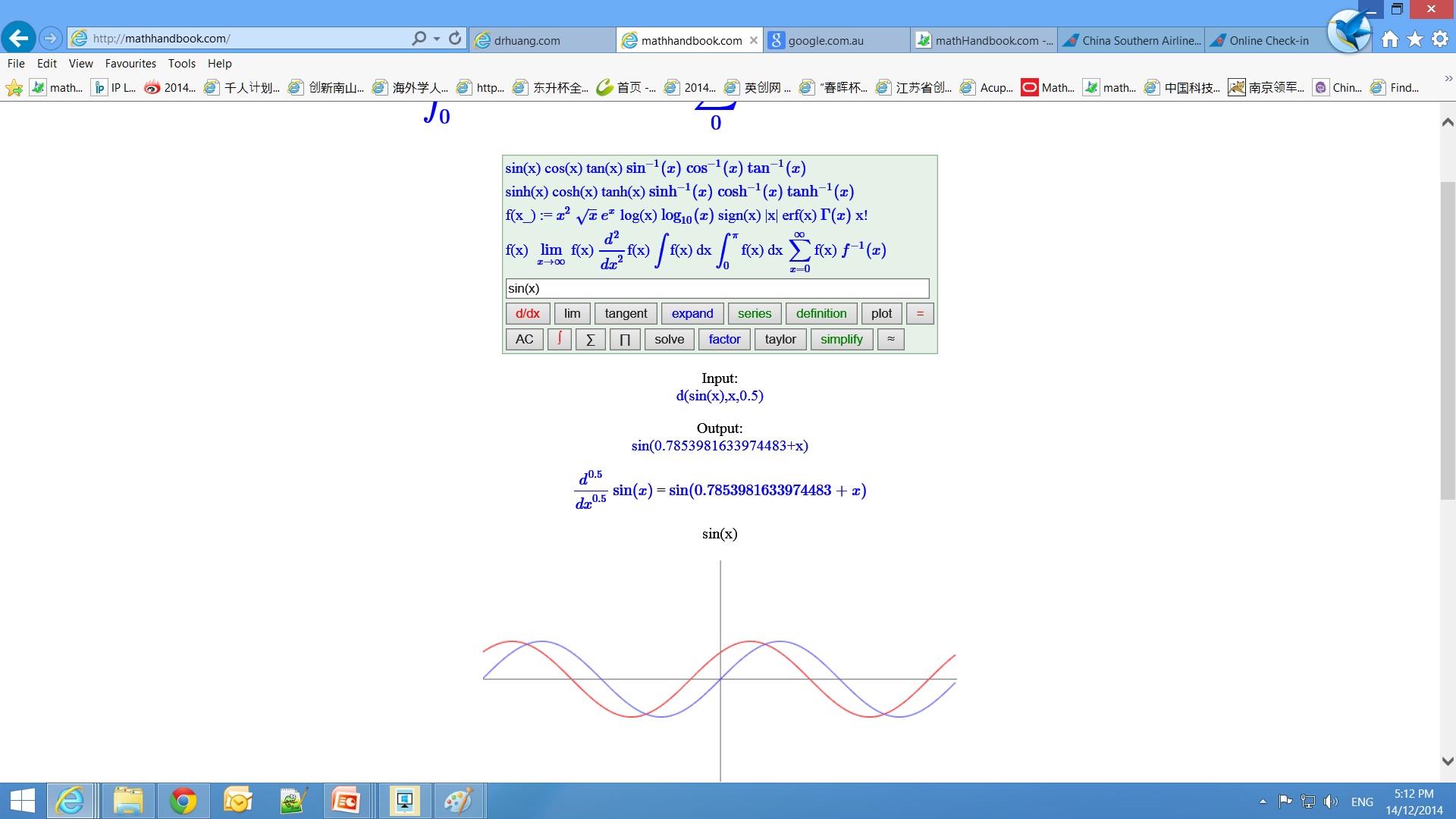
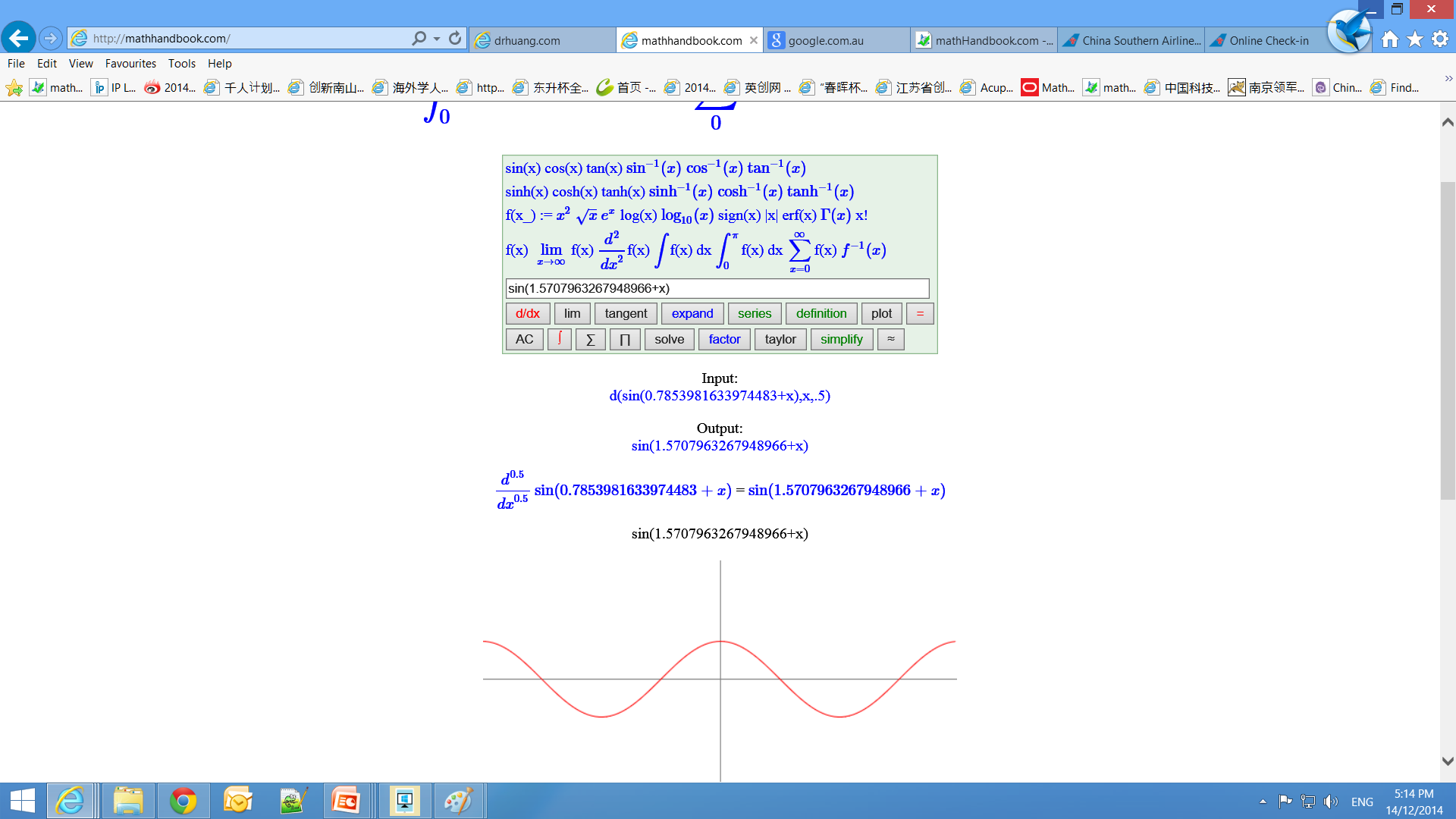
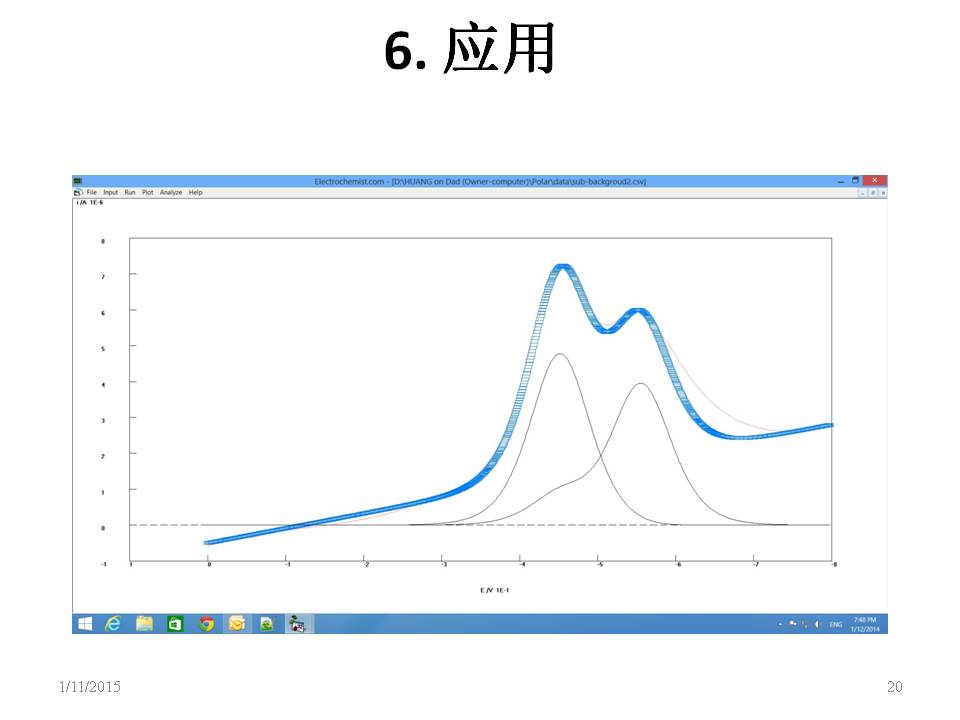
应用 近年来分数阶微积分被广泛的应用于反常扩散、信号处理与控制、流体力学、图像处理、软物质研究、地震分析、粘弹性阻尼器、电力分形网络、分数阶正弦振荡器、分形理论、分数阶PID控制器设计, 电化学. 半微分在电化学的应用 [1-3], 分形理论应用于电化学 [4-6].

参考文献

1. J. Mo, P. Cai, W. Huang and F. Yun, Study on the multiple semi-differential electroanalysis of electrochemical stripping method with thin mercury film formed in situ, J. Zhongshan Uni. (Zhongshan Daxue Xuebao), 1984, (4), 76-84, CA 103: 115269.
2. J. Mo, P. Cai, W. Huang and F. Yun, Theory and application on multiple semidifferential electrochemical stripping analysis with thin mercury film formed in situ, Acta Chimica Sinica, 1984, 42(6), 556-561, CA 101: 162712.
3. J. Mo, W. Huang and R.J. Zhang, New Advances in convolution voltammetry (Review), J. Anal. Determ. (Fenxiceshi Tongbao), 1985, 4(3), 1-8, CA 105: 163910.
4. W. Huang and B. Hibbert, Computer modelling of electrochemical growth with convection and migration in rectangular cell, Phys. Rev. E, 1996, 53(1), 727-730.
5. J. Jiang, W. Huang and B. Hibbert, Determining fractal dimensions of DLA structures using cumulative randic indices, Physica A, 1996, 233(3-4), 884-887.
6. W. Huang and B. Hibbert, Fast fractal growth with diffusion, convection, and migration by computer simulation: Effects of voltage on probability, morphology and fractal dimension of electrochemical growth in a rectangular cell, Physica A, 1996, 233(3-4), 888-896.

书单