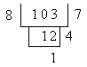5. 实数进位制
[进位制的基与数字] 任一正数可表为通常意义下的有限小数或无限小数,各数字的值与数字所在的位置有关,任何位置的数字当小数点向右移一位时其值扩大10倍,当小数点向左移一位时其值缩小10倍.例如
![]()
一般地,任一正数a可表为
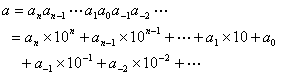
这就是10进数,记作a(10),数10称为进位制的基,式中ai在{0,1,2,L,9}中取值,称为10进数的数字,显然没有理由说进位制的基不可以取其他的数.现在取q为任意大于1的正整数当作进位制的基,于是就得到q进数表示
![]() (1)
(1)
式中数字ai在{0,1,2,L,q-1}中取值,anan-1La1a0称为q进数a(q)的整数部分,记作[a(q)];
a-1a-2L称为a(q)的分数部分,记作{a(q)}.常用进位制,除10进制外,还有2进制、8进制、16进制等,其数字如下
2进制 0, 1
8进制 0, 1, 2, 3, 4, 5, 6, 7
16进制 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
![]()
[2,8,16进制的加法与乘法表]
|
2进制加法表 |
|
2进制乘法表 |
||||
|
+ |
0 |
1 |
|
|
0 |
1 |
|
0 |
0 |
1 |
|
0 |
0 |
0 |
|
1 |
1 |
10 |
|
1 |
0 |
1 |
8进制加法表
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
|
1 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
10 |
|
2 |
02 |
03 |
04 |
05 |
06 |
07 |
10 |
11 |
|
3 |
03 |
04 |
05 |
06 |
07 |
10 |
11 |
12 |
|
4 |
04 |
05 |
06 |
07 |
10 |
11 |
12 |
13 |
|
5 |
05 |
06 |
07 |
10 |
11 |
12 |
13 |
14 |
|
6 |
06 |
07 |
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
07 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
8进制乘法表
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
1 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
|
2 |
00 |
02 |
04 |
06 |
10 |
12 |
14 |
16 |
|
3 |
00 |
03 |
06 |
11 |
14 |
17 |
22 |
25 |
|
4 |
00 |
04 |
10 |
14 |
20 |
24 |
30 |
34 |
|
5 |
00 |
05 |
12 |
17 |
24 |
31 |
36 |
43 |
|
6 |
00 |
06 |
14 |
22 |
30 |
36 |
44 |
52 |
|
7 |
00 |
07 |
16 |
25 |
34 |
43 |
52 |
61 |
16进制加法表
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
0 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
|
1 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
0 |
|
|
|
|
10 |
|
2 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
|
3 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
|
4 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
16进制加法表
|
5 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
|
6 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
|
7 |
07 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
8 |
08 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
9 |
09 |
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
|
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
|
|
|
|
|
16进制乘法表
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
0 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
00 |
|
1 |
00 |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
09 |
|
|
|
|
|
|
|
2 |
00 |
02 |
04 |
06 |
08 |
|
|
|
10 |
12 |
14 |
16 |
18 |
|
|
|
|
3 |
00 |
03 |
06 |
09 |
|
|
12 |
15 |
18 |
|
|
21 |
24 |
27 |
|
|
|
4 |
00 |
04 |
08 |
|
10 |
14 |
18 |
|
20 |
24 |
28 |
|
30 |
34 |
38 |
|
|
5 |
00 |
05 |
|
|
14 |
19 |
|
23 |
28 |
|
32 |
37 |
|
41 |
46 |
|
|
6 |
00 |
06 |
|
12 |
18 |
|
24 |
|
30 |
36 |
|
42 |
48 |
|
54 |
|
|
7 |
00 |
07 |
|
15 |
|
23 |
|
31 |
38 |
|
46 |
|
54 |
|
62 |
69 |
|
8 |
00 |
08 |
10 |
18 |
20 |
28 |
30 |
38 |
40 |
48 |
50 |
58 |
60 |
68 |
70 |
78 |
|
9 |
00 |
09 |
12 |
|
24 |
|
36 |
|
48 |
51 |
|
63 |
|
75 |
|
87 |
|
|
00 |
|
14 |
|
28 |
32 |
|
46 |
50 |
|
64 |
|
78 |
82 |
|
96 |
|
|
00 |
|
16 |
21 |
|
37 |
42 |
|
58 |
63 |
|
79 |
84 |
|
|
|
|
|
00 |
|
18 |
24 |
30 |
|
48 |
54 |
60 |
|
78 |
84 |
90 |
|
|
|
|
|
00 |
|
|
27 |
34 |
41 |
|
|
68 |
75 |
82 |
|
|
|
|
|
|
|
00 |
|
|
|
38 |
46 |
54 |
62 |
70 |
|
|
|
|
|
|
|
|
|
00 |
|
|
|
|
|
|
69 |
78 |
87 |
96 |
|
|
|
|
|
[8-2,16-2数字转换表]
|
8进数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2进数 |
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
|
16进数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2进数 |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
16进数 |
8 |
9 |
|
|
|
|
|
|
|
2进数 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
[各种进位制的相互转换]
1°
q→10转换 适用通常的10进数四则运算规则,根据公式(1),可以把q进数a(q)转换为10进数表示.例如
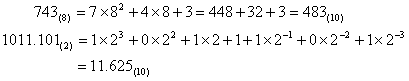
2° 10→q转换 转换时必须分为整数部分和分数部分进行.
对于整数部分其步骤是:
(1) 用q去除[a(10)],得到商和余数.
(2) 记下余数作为q进数的最后一个数字.
(3) 用商替换[a(10)]的位置重复(1)和(2)两步,直到商等于零为止.
对于分数部分其步骤是:
(1)用q去乘{a(10)}.
(2)记下乘积的整数部分作为q进数的分数部分第一个数字.
(3)用乘积的分数部分替换{a(10)}的位置,重复(1)和(2)两步,直到乘积变为整数为止,或直到所需要的位数为止.例如:
103.118(10)=147.074324L(8)
|
整数部分的草式 |
分数部分的草式 |
|
|
|
3° p→q转换 通常情况下其步骤是:a(p)→a(10)→a(q).如果p,q是同一数s的不同次幂,其步骤是:a(p)→a(s)→a(q).例如,8进数127.653(8)转换为16进数时,由于8=23,16=24,所以s=2,其步骤是:首先把8进数的每个数字根据8-2转换表转换为2进数(三位一组)
127.653(8)=001 010 111.110 101 011(2)
然后把2进数的所有数字从小数点起(左和右)每四位一组分组,从16-2转换表中逐个记下对应的16进数的数字,即
![]()