§2 代数方程的性质
一、多项式与代数方程的一般性质
[代数基本定理] 每个复数域上n次代数方程
f(x)=a0xn+a1xn-1+L+an-1x+an=0
(n![]() 1)
1)
在复数域中至少有一个根.
代数基本定理的推论:每个n次代数方程在复数域中有n个根,而且只有n个根.
[多项式的导数] 多项式f(x)的导数为
![]() (x)=na0xn-1+(n-1)a1xn-2+L+an-1
(x)=na0xn-1+(n-1)a1xn-2+L+an-1
微分学中仅考虑实变数函数的导数,而代数学中必须考虑复系数的复变数多项式的导数,但是它们的定义与计算公式仍然一样.
[单根与重根]
1° 多项式的单根不是它的导数的根.
2° 多项式的m重根(即有m个根相同)是它的导数的m-1重根(m>1).
3° 若x1,x2,L,xk分别为f (x)的α1,α2,L,αk(α1+α2+L+αk=n)重根,则
f (x)=a0(x-x1)![]() (x-x2)
(x-x2)![]() L(x-xk)
L(x-xk)![]()
[洛尔定理及其推论] 由微分学中的洛尔定理可知,在实系数方程f (x)=0的两个实根之间总有![]() (x)=0的一个实根.
(x)=0的一个实根.
从这个定理可推出下列两个推论:
1° 若f(x)的一切根都是实的,则![]() (x)的一切根也是实的.在f(x)的相邻两根之间有
(x)的一切根也是实的.在f(x)的相邻两根之间有![]() (x)的一个根并且是一个单根.
(x)的一个根并且是一个单根.
2° 若f(x)的一切根都是实的,且其中有p个(计算重根)是正的,则![]() (x)有p个或
(x)有p个或
p-1个正根.
[多项式的相关]
1° 若多项式f (x),![]() (x)的次数都不超过n,而它们对n+1个不同的数α1,L,
(x)的次数都不超过n,而它们对n+1个不同的数α1,L,![]() 有相等的值,即f(αi)=
有相等的值,即f(αi)=![]() (αi) (i=1,L,n+1),则f (x)=
(αi) (i=1,L,n+1),则f (x)=
![]() (x).
(x).
2° 多项式f (x)和![]() (x)的根完全相同的充分必要条件是f (x)和
(x)的根完全相同的充分必要条件是f (x)和![]() (x)只差一个不等于零的常数因子.
(x)只差一个不等于零的常数因子.
[整根与有理根] 任意整系数方程f (x)=0,若有一个有理根![]() (为既约分数),则p是αn的约数,q是α0的约数.
(为既约分数),则p是αn的约数,q是α0的约数.
由此可推出:任意整系数方程的整根必为常数项的约数,若整系数方程的首项系数为1,则它的有理根必为整数.
[实根与复根,共轭实根与共轭复根]
1° 任意有理系数方程f (x)=0,若有一个根a+![]() (a,b是有理数,
(a,b是有理数,![]() 是无理数),则必有另一个根a-
是无理数),则必有另一个根a-![]() .这时a+
.这时a+![]() 与a-
与a-![]() 称为一对共轭实根.
称为一对共轭实根.
2° 任意实系数方程f (x)=0的复根只可能是成对的共轭复根,并且根的重数相同.从而,复根的个数是偶数.
3° 任意实系数奇数次方程f (x)=0至少有一个实根.
4° 任意实系数偶数次方程f (x)=0,a0an<0,则至少有两个实根(一个正根和一个负根).
[根与系数的关系] 设
f (x)=xn+a1xn-1+L+an
为复数域S上的一元多项式,x1,x2,L,xn为f (x)在S中的n个根,则根与系数的关系为
x1+x2+L+xn=![]() =-a1
=-a1
x1x2+x1x3+L+xn-1xn=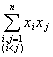 =a2
=a2
x1x2x3+x1x2x4+L+xn-2xn-1xn=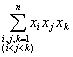 =-a3
=-a3
LLLLLL
x1x2Lxn=(-1)nan
这就是说,f (x)的xn-k的系数ak等于从它的根x1,x2,L,xn中每次取k个(不同的)一切可能乘积之和,若k是偶数,则取正号,若k为奇数,则取负号.
[根的范围] 设ξ为复系数代数方程
f (x)=a0xn+a1xn-1+L+an-1x+an=0 (1)
的根.
1° 若所有系数ai![]() 0 (i=0,1,L,n),则
0 (i=0,1,L,n),则![]() ,其中
,其中![]() 为实系数代数方程
为实系数代数方程
F(x)=![]() xn-
xn-![]() xn-1-L-
xn-1-L-![]() =0
=0
的一个正实根.
2° 设γ1,γ2,L,γn-1为任意正数,则![]() τ,其中τ为下列n个数中最大的一个:
τ,其中τ为下列n个数中最大的一个:
![]() +
+![]() ,
, ![]()
![]() +
+![]() , L,
, L, ![]()
![]() L
L![]() +
+![]() ,
,
![]()
特别,取γi=1(i=1,2,L,n-1)时,有
![]() max
max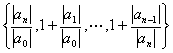 (2)
(2)
方程(1)中作变换x=![]() ,可求出
,可求出![]() 的上界,因而得到
的上界,因而得到
![]()
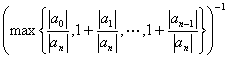 (3)
(3)
更进一步,记(2)式右边为M,记(3)式右边为m,如果取ρ<M,使得
![]()
![]()
![]() L
L![]()
![]()
取![]() >m,使得
>m,使得
![]()
![]() L
L![]()
![]()
那末有![]()
![]() .
.
3° 设γ为任意正数,则![]() ,其中
,其中
τ1=max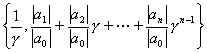
特别,取γ=1,有
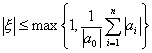
4° 若所有系数都为正实数,则
min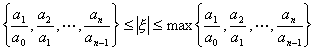
5° 若方程(1)的系数满足不等式
![]()
则方程(1)至多有一个绝对值≥1的根ξ1,而且
![]()
[多项式的分解]
1° 设f (x)为实数域上的多项式,若有非常数的实系数多项式g(x)和h(x),使得
f (x)=g(x)h(x)
则称f (x)为实数域上可约(或可化),否则称f(x)为实数域上的不可约多项式.
2° 实数域上不可约多项式,除一次多项式外,只有含(共轭)复根的二次多项式.
3° 每个实系数多项式都可分解为实系数的一次因式与二次因式之积.
有理数域上的多项式的分解见第二十章,§5,2.
[余数定理与综合除法] 若c为一常数,则多项式f (x)除以x-c所得的余数等于f(c).
设 f (x)=a0xn+a1xn-1+L+an-1x+an
求f (x)除以x-c的商式与余数其计算格式如下:
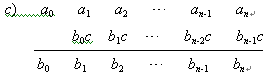 |
式中b0=a0,bi=ai+bi-1c(i=1,2,L,n).于是得到
商式 q(x)=b0xn-1+b1xn-2+L+bn-1
余数 r=bn=f(c)
例 f (x)=![]() 除以
x-2. 列出算式
除以
x-2. 列出算式
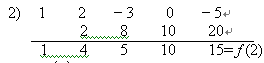 |
所以 ![]()
[多项式的泰勒公式(秦九韶法)] n次多项式
f (x)=a0xn+a1xn-1+L+an-1x+an (a0![]() 0)
0)
在任意点c的泰勒展开式为
f (x)=b0(x-c)n+b1(x-c)n-1+L+bn-1(x-c)+bn
式中系数bi (0≤i≤n)按下面的方法计算.
首先在(n+2)![]() (n+2)方阵的对角线上列出a0,a1,L,an,d(d为符号),在第1列上列出a0(即ai,i=ai-1,i=1,2,L,n+1;an+2,n+2=d;ai,1=a0,i=1,2,L,n+2).
(n+2)方阵的对角线上列出a0,a1,L,an,d(d为符号),在第1列上列出a0(即ai,i=ai-1,i=1,2,L,n+1;an+2,n+2=d;ai,1=a0,i=1,2,L,n+2).
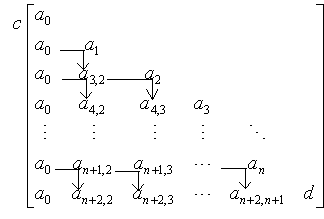 |
然后再按递推公式
ai,jc+ai,j+1=ai+1,j+1 (i=2,L,n+1; j=1,L,i-1)
自上而下,自左而右依次计算出对角线下其余各元素,那末第n+2行各元素即为所求系数,即
b0=a0, bi=an+2,i+1 (i=1,2,L,n)
例 求f (x)=![]() 在x=2处的泰勒展开式.
在x=2处的泰勒展开式.
解
![]()
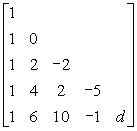
则
f (x)=![]()