二、多元多项式·对称多项式·结式

[多元多项式] 设常数c₁,c₂,L,c_k属于一个数域S,α_i,β_i,L,ν_i(i=1,2,L,k)是正整数或零，则称形如

L +

的表达式为数域S上元素x₁,x₂,L ,x_n的n元多项式.称为它的项，c_i为它的系数，α_i为项中关于x₁的次数，β_i为项中关于x₂的次数,等等.α_i+β_i+L+为项的次数.在多项式中系数不为零的任一项关于x_i的最高次数称为多项式关于x_i的次数，系数不为零的任一项的最高次数叫做多项式的次数.各项次数都相等的多项式称为齐次多项式.

每个m次多项式f(x₁,x₂,L,x_n)都可唯一地表示成

f(x₁,x₂,L,x_n)=

式中f_i(x₁,x₂,L,x_n)为i次齐次多项式.

为了方便，经常把一个多元多项式按某一个变数，例如x₁的降幂排列如下：

a₀(x₂,L,x_n)x₁^m+a₁(x₂,L,x_n)x₁^m-1+L+a_m(x₂,L,x_n)

式中a₀(x₂,L,x_n),a₁(x₂,L,x_n),L,a_m(x₂,L,x_n)为x₂,L,x_n的n－1元多项式.

若f₁,f₂,L,f_k分别为m₁,m₂,L,m_k次的多元多项式，则乘积f₁f_2Lf_k为m₁+m₂+L+m_k次.

[对称多项式] 如果在一个n元多项式f(x₁,x₂,L,x_n)中，对调任一对x_i和x_j后，f(x₁,x₂,L,x_n)不变，那末称它为x₁,x₂,L,x_n的对称多项式.

[初等对称多项式] 设

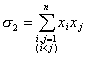
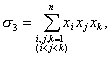
L L L L L L σ_n=x₁x_2L x_n

则称σ₁,σ₂,L ,σ_n为初等对称多项式.例如，由多项式的根与系数的关系（本节，一）可知，多项式的系数除符号外都是根的初等对称多项式.

[对称多项式基本定理] 在数域S上，每个n元对称多项式f(x₁,L,x_n)都可唯一地表成x₁,L,x_n的初等对称多项式（系数在S中）的多项式.

[牛顿公式] 设

f(x)=(x－x₁) (x－x₂)L (x－x_n)=xⁿ－σ₁x^n－1+L +(－1)ⁿσ_n

s_k=x₁^k+x₂^k+L+x_n^k (k=0,1,2,L)

则下面牛顿公式成立：

k≤n时,s_k－σ₁s_k-1+σ₂s_k-2+L+(－1)^k-1σ_k-1s₁+(－1)^kkσ_k =0

k>n时，s_k－σ₁s_k-1+σ₂s_k-2+L+(－1)ⁿσ_ns_k-n=0

[结式] 设

f(x)=a₀x^m+a₁x^m－1+L+a_m=a₀ (m>0)

j (x)=b₀xⁿ+b₁x^n－1+L+b_n=b₀ (n>0)

则

R(f,j )=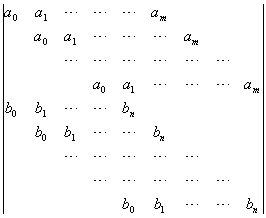

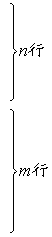
这个m+n阶行列式R(f,j)称为多项式f(x)和j(x)的结式，式中空白处的元素都是零.结式具有性质：

R(f,j)=(－1)^mn R(j,f)

R(f,j)=

设a₀,b₀不全为零，则f(x),j(x)在复数域上有公共根的充分必要条件是它们的结式R(f,j)=0.

行列式R(f,j)是f(x)与j(x)的系数的一个m+n次齐次多项式，关于a₀,a₁,L,a_m是n次齐次多项式，关于b₀,b₁,L ,b_n是m次齐次多项式.