1.基本概念与基本性质
[级数的基本概念]设![]() ,
,![]() ,是一个无穷序列,符号
,是一个无穷序列,符号
![]()
称为无穷级数,简称级数,记作![]() .an称为级数的一般项.
.an称为级数的一般项.
An= a1+a2+![]() (n=1,
(n=1,![]() )
)
称为级数的第n个部分和.若当n![]() ∞时,部分和序列{An}具有有穷或无穷(但有确定的正号或负号的)极限A:
∞时,部分和序列{An}具有有穷或无穷(但有确定的正号或负号的)极限A:
A=![]() An=
An=![]()
![]()
则称A为级数的和,并写成
A= a1+a2+![]()
![]()
若级数具有有穷和,则称级数为收敛的,否则,即级数和等于±∞,或不存在,则称级数为发散的.
[级数的基本性质]
(1) 弃去级数前面的有限项或在级数前面加进有限项,并不影响级数的收敛与发散的性质.
(2) 若级数![]() 收敛,则它的第m项后的余项的和数
收敛,则它的第m项后的余项的和数
am=am+1+am+2+![]()
当m![]() ∞时趋于零.
∞时趋于零.
(3) 若级数![]() 收敛,c是任一常数,则级数
收敛,c是任一常数,则级数![]() 也收敛,并有
也收敛,并有
![]() =c
=c![]()
(4) 若![]() 与
与![]() 都收敛,则
都收敛,则![]() 也收敛,并有
也收敛,并有
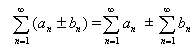
[柯西准则] 级数![]() 收敛的充分必要条件是:对任意的ε>0,都存在正整数N=N(ε),使得当n
收敛的充分必要条件是:对任意的ε>0,都存在正整数N=N(ε),使得当n![]() N时,对一切正整数p,下列不等式成立:
N时,对一切正整数p,下列不等式成立:
![]()
[级数收敛的必要条件] 级数![]() 收敛的一个必要条件是:一般项an趋于零,即
收敛的一个必要条件是:一般项an趋于零,即![]() an=0.
an=0.