§3   微  分

一、单变量函数的微分

    1. 基本概念

[导数的定义及其几何意义]  设函数y=f(x)当自变量在点x有一改变量时,函数y相应地有一改变量 ,那末当趋于零时,若比的极限存在(一确定的有限值)，则称这个极限为函数f(x)在点x的导数,记作

这时称函数f(x)在点x是可微分的函数(或称函数f(x)在点x可微)。

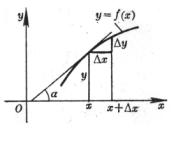
在几何上,函数f(x)的导数是函数y=f(x)表示的曲线在点x的切线的斜率,即

=

式中α为曲线在点x的切线与x轴的夹角(图5.1)。

    [单边导数]

=

及

=

分别称为函数f(x)在点x的左导数和右导数。

导数存在的充分必要条件是:

=

    [无穷导数]  若在某一点x有

=±∞

则称函数f(x)在点x有无穷导数。这时函数y=f(x)的图形在点x的切线与x轴垂直(当=

+∞时,函数f(x)的图形在点x的切线正向与y轴方向一致,当=－∞时,方向相反)。

    [函数的可微性与连续性的关系]  如果函数y=f(x)在点x有导数，那末它在点x一定连续。反之,连续函数不一定有导数,例如

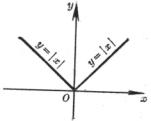
    1°　函数y=|x|在点x=0连续,在点x=0,左导数=－1,右导数 =1,而导数

不存在(图5.2)。

图5.2              图5.3

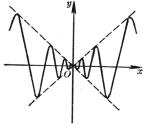
    2°　函数

                     y=f(x)=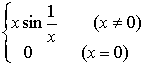 

在点x=0连续,但在点x=0左右导数都不存在(图5.3)。