2. 求导数的基本法则
[四则运算求导公式] 若c为常数,函数u=u(x),![]() 都有导数,则
都有导数,则
![]() =0
=0
![]() =c
=c![]()
![]()
![]()
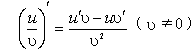
[复合函数的导数] 若y=f(u),u=![]() 都有导数,则
都有导数,则
![]() =
=![]()
[反函数的导数] 如果函数y=f(x)在点x有不等于零的导数,并且反函数x=f-1(y)在点y连续,那末![]() 存在并且等于
存在并且等于![]() ,即
,即
![]() =
=![]()
[隐函数的导数] 假定函数F(x,y)连续,并且对于每个自变量都有连续的偏导数,而且![]() ,则由
,则由
F(x,y)=0
所决定的函数y=f(x)的导数
![]() =
=![]() =
=![]()
式中![]() =
=![]() ,
,![]() =
=![]() (见本节,四)。
(见本节,四)。
[用参数表示的函数的导数] 设方程组
![]() (α<t<β)
(α<t<β)
式中![]() 和
和![]() 为可微分的函数,且
为可微分的函数,且![]() ,则由隐函数存在定理(本节,四,1)可把y确定为x的单值连续函数
,则由隐函数存在定理(本节,四,1)可把y确定为x的单值连续函数
y=![]()
而函数的导数可用公式
![]() =
=![]()
求得。
[用对数求导数法] 求一函数的导数,有时先取其对数较为便利,然后由这函数的对数求其导数。
例 求
![]()
的导数。
解 两边各取对数,得
lny=pln(x-a)+qln(x-b)-rln(x-c)
左边的lny为y的函数,而y又为x的函数,故应用求复合函数的导数的法则得到
![]()
由此得
![]()
所以
![]()