3．约束条件为等式的条件极值

   求函数

y = f (x),  x=(x₁,x₂)

在m(m<n)个约束条件

g_k(x)=0,  k =1,2,

下的极值.

[直接代入法]  从约束条件的m个方程中将其m个变量解出，用其余n-m个变量表示，然后直接代入函数中去，这样就变为一个求n－m个变量的函数的无约束条件的极值问题.如果从约束方程能够将m个变量解出，这个方法是可行的.

[拉格朗日乘数法]  引进修正的系数

F=y+

式中λ_k为待定常数.把F当作n+m个变量x₁,x_n和λ₁,λ₂,的无约束的函数，对这些变量求一阶偏导数得稳定点所要满足的方程：

，  i =1,,n

g_k=0,   k =1,2,

例1  求函数

y =

在约束条件

2x₁+3x₂=6

下的极值.

解  由于

y =

和                                                      g =2x₁+3x₂－6=0

可知修正的函数为

F = ()+λ(2x₁+3x₂－6)

解方程组

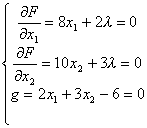
得                                             λ＝，x₁=,x₂=

所以函数F的稳定点为

x₁=,    x₂=

由于                            D₁== 8 >0

D₂==80>0

这是一个极小点，函数y的极小值为.

［惩罚函数法］ 在搜索极小点时引进修正函数

F = y+                                                    (1)

式中P_k是任意大的正整数，称为惩罚函数.这样就可把问题化为新函数F的无条件极值问题，可以用不断增大P_k的数值来极小化.也可引进如下形式的新函数

F = y+      

式中P_k是任意大的正整数.

对搜索极大点时，惩罚函数前取负号，即引进新函数

F = y－

或                                                       F = y－    

例２　用惩罚函数法解例１.

解　利用方程（1）引进修正函数

F = y+P(g)²=

解方程组

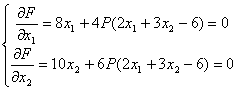
得                                      x₁=x₂，x₂=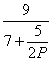

当P很大时，x₂趋于，x₁趋于，这就是稳定点.由于

D₁==8(1+P)>0

D₂==16(5+14P)>0

所以稳定点是一个极小点，这和例1的结果一致.