这一章综述了单变量函数的常义积分、广义积分、含参数积分的基本概念、性质和计算方法，收集了求不定积分、定积分、多重积分、曲线积分、曲面积分的有关公式，主要的积分不等式以及积分的某些近似计算公式，简要地列举了积分在实际中的各种应用；编制了不定积分表和定积分表.
［不定积分（原函数）］ 如果在给定的区间[a ,b]上
那末F (x)称为f(x)在区间[a,b]上的一个原函数.
如果f(x)有一个原函数F (x)，那末它一定有无穷多个原函数，它们是形如
（式中C是任意常数）的函数族，所以用记号
表示f(x)的原函数全体，称为f(x)的不定积分.
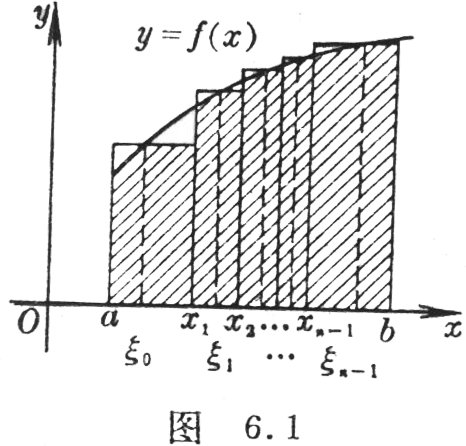
［定积分·黎曼积分］ 设在区间[a,b]上给定了函数f(x).用任意方法把区间[a,b]分成若干部分，其分点为
，并设λ是
(i=0,1,2,…,n－1)中最大的.在每一个小区间[
]上任取一点
(i=0,1,2,…,n－1),作和
（图6.1）.当λ→0时，如果极限
存在，那末这个极限称为函数f(x)在区间[a,b]上的定积分，记作
此时，函数f(x)称为区间[a,b]上的可积函数（黎曼可积），a和b分别称为积分的下限和上限，f(x)称为被积函数，x是积分变量，“
”是积分号.
［牛顿－莱布尼茨公式］ 若函数f(x)在区间[a,b]上连续，或分段连续，则f(x)在[a,b]上有原函数，设F(x)是f(x)在[a,b]上的一个原函数，则
这称为牛顿－莱布尼茨公式，或微积分学基本定理，它指出了定积分与不定积分的内在联系.
［可积函数及其性质］
(１) 若函数f(x)在区间[a,b]上连续，则f(x)是可积的.
(２) 若函数f(x)在[a,b]上有界，且只有有限多个间断点，则f(x)是可积的.
(３) 单调有界函数一定是可积的.
(４) 可积函数一定是有界的.
(５) 若函数f(x)可积，则|f(x)|与kf(x)（k为常数）也可积.
(６) 若函数f(x)，g(x)可积，则其和、差、乘积也可积.
(７) 若函数f(x)在[a,b]上可积，则f(x)在[a,b]中的任一部分区间[α,β]上也可积.反之，若把[a,b]分割成若干部分区间，并分别在每个部分区间上f(x)可积，则它在整个区间[a,b]上可积.
［积分中值定理］儍儍儍儍
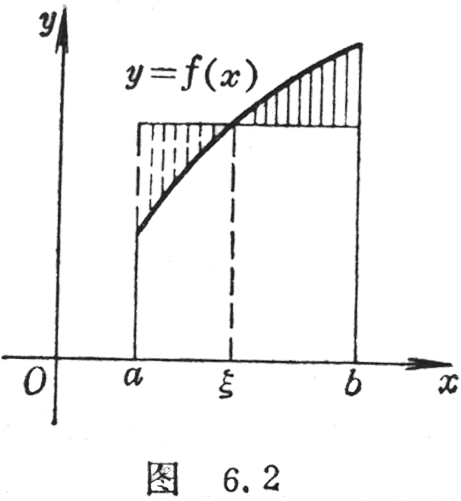
(１) 若函数f(x)在区间[a,b]上连续（图6.2），则在区间[a,b]内至少存在一个数ξ(a<ξ<b)，使得
(２) 若函数f(x)，g(x)在区间[a,b]上有界且可积，f(x)连续，g(x)在区间[a,b]内不变号，则在区间[a,b]内至少存在一个数ξ(a<ξ<b)，使得
这称为关于积分的第一中值定理.
(３) 若函数f(x)，g(x)在区间[a,b]上有界且可积，而f(x)在[a,b]上是单调的，则在区间[a,b]内至少存在一个数ξ(a<ξ<b)，使得
这称为关于积分的第二中值定理.
(４) 除此条件而外，若f(x)非负单调下降（广义的），则
(a<ξ<b)
若f(x)非负单调上升（广义的），则
(a<ξ<b)