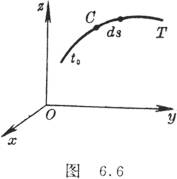
二、 曲线积分
|
|
[对弧长的曲线积分] 若函数f(x,y,z)在光滑曲线C:
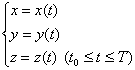
的各点上有定义并且连续(图6.6)则
![]()
式中ds为弧的微分,![]() 等.这个积分与曲线C的方向无关.
等.这个积分与曲线C的方向无关.
[对坐标的曲线积分] 若函数P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)在光滑曲线C:
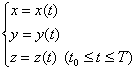
的各点上连续,这曲线的正方向为t增加的方向,则
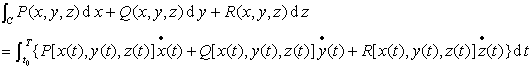
当曲线C的正向变更时,积分的符号改变.
[全微分的情形] 若函数P=P(x,y,z),Q=Q(x,y,z),R=R(x,y,z)在区域V中的任一条光滑曲线C上连续,并且
![]()
式中u=u(x,y,z)为区域V内的单值可微函数,则
![]()
式中(![]() )为积分曲线C的始点,(
)为积分曲线C的始点,(![]() )为积分曲线C的终点.这说明在假定的条件下,积分值与曲线C的形状无关,只与曲线的始点和终点有关(图6.7).
)为积分曲线C的终点.这说明在假定的条件下,积分值与曲线C的形状无关,只与曲线的始点和终点有关(图6.7).
在单连通区域V内有连续的一阶偏导数的函数P,Q,R能表成全微分
![]()
的充分必要条件是:在区域V内等式
![]()
成立.这时函数u可按下面公式求得:
![]()
式中(![]() )为区域V内的某一固定点.
)为区域V内的某一固定点.
|
|
[格林公式]
1°曲线积分与二重积分的关系.设C为逐段光滑的简单(无自交点)闭曲线,围成单连通的有界区域S,这围线的方向使区域S保持在左边,若函数P(x,y),Q(x,y)及它们的一阶偏导数在S+C上连续,则有格林公式 :
![]()
|
|
2° 曲线积分与积分线路的关系.若函数P,Q,![]() 在区域S上连续,且
在区域S上连续,且
![]()
则沿S内的任一光滑闭曲线的积分为零,即
![]()
因而由S中的A到B的积分与线路无关(图6.8),即
![]()