|
方 程 与 图 形 |
说 明 |
|||||
|
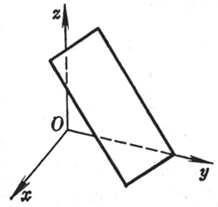
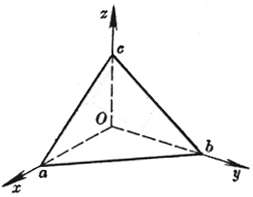
[截距式] |
|
a, b, c分别称为平面在三条坐标轴上的截距 |
||||
|
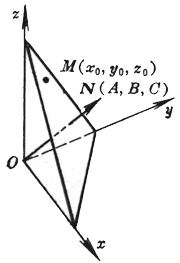
[点法式]
(A, B, C不同时等于零)
|
|
平面通过点M(x0, y0, z0),且法线N的方向数为A, B, C
|
||||
|
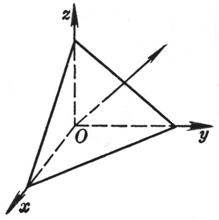
[三点式] |
|
平面通过三点: M1(x1, y1, z1) M2(x2, y2, z2) M3(x3, y3, z3) |
||||
|
或
|
||||||
|
方 程 |
与 图 形 |
说 明 |
||||
|
[一般式] Ax +By +Cz +D = 0 (A, B, C为该平面的法线的方向数,且不同时等于零) |
|
当D=0时,平面通过原点 当A=0时(或B=0,或C=0)时,平面与x轴(或y轴,或z轴)平行 当A=B=0时(或A=C=0,或B=C=0)时,平面与Oxy平面(或Ozx,或Oyz)平行 |
||||
|
[法线式] (a , b , g 为平面的法线的方向角,p³ 0为法线长即原点到平面的距离)
|
|
平面的一般式可化为法线式 |
||||
|
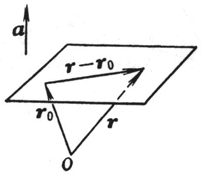
[矢量式] (r -r0)× a = 0 |
|
平面 通过矢径r0的终点,且与已知矢量a垂直,r为平面上任意一点的矢径 |
||||
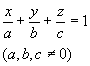
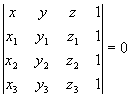
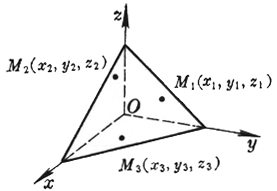
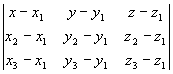 =0
=0