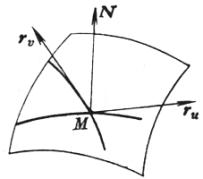
八、    曲面的基本公式与基本方程

       [高斯公式与外因格尔登公式]  设曲面的参数方程为，在曲面上每点M取三个不共面的矢量，由这三个矢量组成的三面形称为曲面的活动标架或伴随三面形；要注意，在这里和不互相垂直，但它们都在切面上而垂直于法线单位矢量N.

       可以把关于u，的偏导数表示为下列形式的线性组合：

                                      （1）

                               （2）

式中E，F，G和L，M，N分别为曲面的第一和第二基本量；六个系数称为第一基本二次型的第二类克里斯托弗尔记号，它们的表达式是

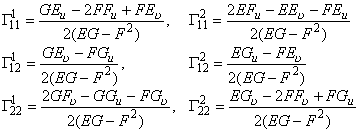
方程组（1）称为曲面的偏微分方程，又称为高斯公式；方程组（2）称为外因格尔登公式；（1），（2）合称为曲面的基本公式，这些公式的特点是，把矢量的导数用矢量本身的线性组合来表达，其系数仅与曲面的第一、第二基本量有关.

       [高斯方程与柯达奇方程]  方程组（1）的可积条件为

                                （3）

和         

                                    （4）

       方程组（2）的可积条件是（4）.方程组（4）成为柯达奇方程.

从（3）可以得到下列定理：

       1 、高斯定理  曲面的总曲率K可以用第一基本量和它们的一阶，二阶偏导数来表示；因而总曲率是曲面的一个等距不变量.

       2、在等距对应下，曲面的对应点必有相同的总曲率.

       这个重要结果表明，总曲率不同的两个曲面具有很大的差别性，即使允许曲面经过任意的弯曲，也不能使这两个曲面互相贴合.

       总曲率K以E，F，G的表达式称为高斯方程，与柯达奇方程合并起来称为曲面的基本方程.

       [波恩涅定理]  给定任意两个二次型

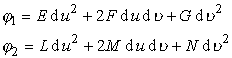
其中是正定的，假定和的系数满足高斯方程和柯达奇方程，则除了空间位置的差别外，唯一地存在一个曲面，以和分别作为它的第一和第二基本二次型.