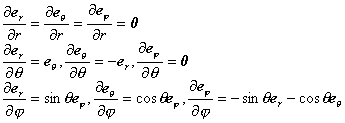二、 梯度、散度、旋度在不同坐标系中的表达式
1.单位矢量的变换
[一般公式] 假定x=f(![]() ),y=g(
),y=g(![]() ),z=h(
),z=h(![]() )把(
)把(![]() )空间的一个区域 一对一地连续映射为(x,y,z)空间的一个区域D,并假定f,g,h都有连续偏导数,因为对应是一对一的,所以有
)空间的一个区域 一对一地连续映射为(x,y,z)空间的一个区域D,并假定f,g,h都有连续偏导数,因为对应是一对一的,所以有
![]()
![]() =
=![]() (x,y,z),
(x,y,z),![]()
再假定![]() 也有连续偏导数,则有
也有连续偏导数,则有

或逆变换
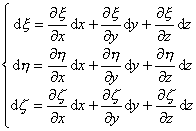
沿dx,dy,dz方向的单位矢量记作i,j,k,沿![]() 方向的单位矢量记作
方向的单位矢量记作![]() ,则有
,则有
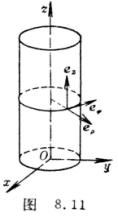
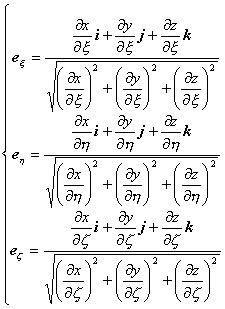
[圆柱面坐标系的单位矢量] 对于圆柱面坐标系(图8.11)
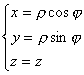
![]()
单位矢量为
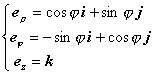
它们的偏导数为
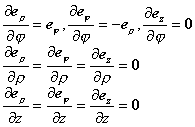
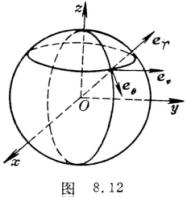
[球面坐标系的单位矢量] 对于球面坐标系(图8.12)
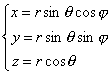
![]()
单位矢量为
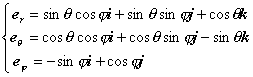
它们的偏导数为