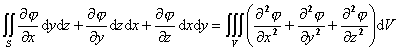四、 矢量的积分定理
[高斯公式]
![]() RdV=
RdV=![]() R·dS=
R·dS=![]() R·NdS
R·NdS
即
![]()
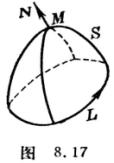 式中S为空间区域V的边界曲面,N=
式中S为空间区域V的边界曲面,N=![]() 为
为
在S上一点的法线单位矢量,R(r)=(X(x, y,z),Y(x, y,z),Z(x, y,z))
在V+S上有连续偏导数.
[斯托克斯公式]
![]() rot
R·dS=
rot
R·dS=![]() rot
R·NdS=
rot
R·NdS=![]() R·dr
R·dr
即
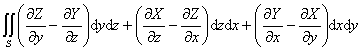
= 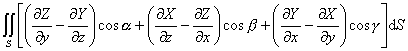
= ![]()
式中S为一定曲面的一侧,L为曲面S的闭边界曲线(L的正向与N构成右手系).S的每点有切面,其方向连续地依赖于曲面上的点,而边界曲线L上的每点都有切线(图8.17). R(r)=(X(x, y,z),Y(x, y,z),Z(x, y,z))在曲面的所有点单值,并在与S足够靠近的点处有连续偏导数.
[格林公式]
![]() ·dS=
·dS=![]()
![]() ·dS=
·dS=![]()
式中S为空间区域V的边界曲面,![]() 为两个标函数,在S上具有连续偏导数,且在V上具有二阶连续偏导数,
为两个标函数,在S上具有连续偏导数,且在V上具有二阶连续偏导数,![]() 为拉普拉斯算子,特别
为拉普拉斯算子,特别
![]() ·dS=
·dS=![]()
即