§4   张量算法

一、 张量概念

    [张量的一般定义]  若一个量有n^N个分量，而每个分量在n维空间Rⁿ中的坐标变换

    (i= 1 , ···, n)

之下，按下面的规律变化：

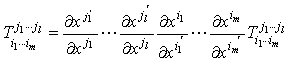
式中是xⁱ的函数，是的函数，则量(共有n^N个分量)称为l阶逆变(或抗变)m阶协变的N(=l＋m)阶混合张量(或称为(l＋m)型混合张量).

    张量概念是矢量和矩阵概念的推广，标量是零阶张量，矢量是一阶张量，矩阵(方阵)是二阶张量，而三阶张量(例如)好比“立体矩阵”(图8.18右).更高阶的张量不能用图形表达.下面列出n=2时的张量示意图：

    [张量举例]

    1  可乘张量  设由逆变分量和协变分量所给定的两个矢量a , b是已知的，则由等式

  确定的都是二阶张量，称为可乘张量.

    2  克罗内克尔符号   克罗内克尔符号是一阶逆变一阶协变的二阶混合张量，这是因为从

可得

    [二阶对称张量与反对称张量]  若张量满足等式

则分别称为二阶对称协变张量、二阶对称逆变张量和二阶对称混合张量.若张量满足等式

则分别称为二阶反对称协变张量、二阶反对称逆变张量和二阶反对称混合张量.

    张量的逆变(协变)指标的对称性质在坐标变换下是不变的.

在三维空间中，二阶反对称张量与矢量等价.