三、    黎曼空间中的曲率

[曲率张量与李奇公式]  张量的协变导数与普通导数的明显区别是：求高阶导数时，张量导数的结果一般与求导的次序有关.例如，运算作用于矢量时，则有         

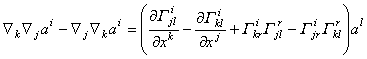                (1)

记

它是一个三阶协变一阶逆变的四阶混合张量，称为空间Vⁿ的曲率张量或黎曼－克里斯托弗尔张量.由(1)式得

左边称为逆变矢量的交错二阶协变导数；对协变矢量的交错二阶协变导数是

张量的交错二阶协变导数是

这称为李奇公式.

    [黎曼符号·李奇张量·曲率标量·爱因斯坦空间]

    曲率张量的协变分量

称为第一类黎曼符号，而称为第二类黎曼符号.

    曲率张量缩并得

称为李奇张量.李奇张量再缩并得

R = g^kl R_kl

称为曲率标量.

    若李奇张量满足

则称此空间为爱因斯坦空间.

    [曲率张量的性质]

    1  曲率张量前两个指标j和k是反对称的，即

特别       

    2  曲率张量对三个协变指标作循环置换后相加，使得

这称为李奇恒等式.

    3  第一类黎曼符号R_kjlr可按下式计算：

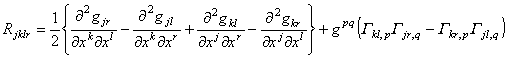
    因此R_kjlr关于指标j , k与 l , r是反对称的；关于前一对指标与后一对指标是对称的；对前面三个指标作循环置换后相加等于零，即

R_jklr =－R_kjlr

R_jklr =－R_jkrl

R_jklr = R_lrjk

R_jklr ＋R_kljr＋R_ljkr = 0

４  李奇张量是对称的，即R_kl = R_lk.

    5  空间Vⁿ中任一点下式成立：

这称为皮安奇恒等式.它表明，按协变导数的指标(i)及曲率张量前两个指标(j , k)作循环置换所得到的和等于零.

    [黎曼曲率(截面曲率)与常曲率空间]  对黎曼空间Vⁿ内一点M的两个线性无关矢量和作

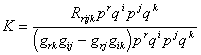
这称为pⁱ，qⁱ所确定的平面的黎曼曲率，又称为截面曲率.

    如果对空间Vⁿ(n > 2)中所有点都有

R_rijk=K(g_rkg_ij－g_rjg_ik)

则黎曼曲率K为常数，这就是舒尔(Schur)定理.

    黎曼曲率为常数的空间Ｖⁿ称为常曲率空间，这种空间的线素可化为形式

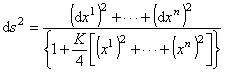
这称为黎曼形式的常曲率空间的度量.

    常曲率空间是爱因斯坦空间.