二、酉空间上的特殊线性变换
[共轭变换] 对域F上酉空间V上的一个线性变换L,由关系式
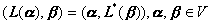
所定义的变换![]() 是线性变换,
是线性变换, ![]() 称为L的共轭变换. 若
称为L的共轭变换. 若![]() ,则称L为正规变换.
,则称L为正规变换.
共轭变换有以下性质:
1o![]()
2o![]()
3o![]()
4o![]()
5o若L是非奇异线性变换,则![]() 也是非奇异线性变换,并且
也是非奇异线性变换,并且
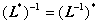
6o若在某一标准正交基下L的矩阵为A,则共轭变换![]() 关于这同一基底的矩阵为A的共轭转置矩阵
关于这同一基底的矩阵为A的共轭转置矩阵![]() .
.
[自共轭变换(埃尔米特变换)] 若![]() ,则称L为自共轭变换或埃尔米特变换.
,则称L为自共轭变换或埃尔米特变换.
自共轭变换有以下性质:
1o若L,M为自共轭变换,![]() 则
则![]() 也是自共轭变换. 当L,M可交换时,LM也是自共轭变换.
也是自共轭变换. 当L,M可交换时,LM也是自共轭变换.
2o在标准正交基下,自共轭变换的矩阵是埃尔米特矩阵. 反之,线性变换关于一标准正交基的矩阵是埃尔米特矩阵,则必为自共轭变换.
3o自共轭变换的特征值是实的.
4o有适当的标准正交基使自共轭变换L对应于一个实对角线矩阵,其主对角线上的元素是L的全部特征值.
[酉变换] 若对酉空间V中的任意![]() ,有线性变换L,使
,有线性变换L,使
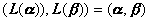
则称L为酉变换.
酉变换有以下性质:
1o恒等变换为酉变换.
2o若L,M为酉变换,则LM也为酉变换.
3o若L为酉变换,则![]() 也为酉变换.
也为酉变换.
4oL为酉变换的充分必要条件是:
![]() 或
或 ![]()
5o在标准正交基下,酉变换L的矩阵是酉矩阵. 反之,线性变换关于一标准正交基的矩阵是酉矩阵,则必为酉变换.
6o酉变换的特征值的绝对值都是1.