三、方阵标准化的方法与步骤
[λ矩阵] 假定一个n阶方阵A的元素都是变数λ的复系数多项式![]()
则![]() 称为λ矩阵. 一个λ矩阵
称为λ矩阵. 一个λ矩阵![]() 的不恒等于零的子式的最高阶数r称为
的不恒等于零的子式的最高阶数r称为![]() 的秩.
的秩.
[不变因子与初等因子] 设r为![]() 的秩,k是正整数
的秩,k是正整数![]() ,
,![]() 为
为![]() 的一切k阶子式的最高公因式,则
的一切k阶子式的最高公因式,则![]() 是一个
是一个![]() 的多项式,规定
的多项式,规定![]() 的
的![]() 最高次项系数是1;此外规定
最高次项系数是1;此外规定
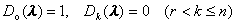
称
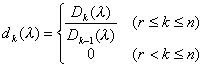
为![]() 的不变因子.
的不变因子.
把每个![]() 分解为一次因子,得到
分解为一次因子,得到
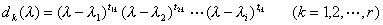
式中指数![]() 有的可能是零,当
有的可能是零,当![]() 时,
时,![]() 称为
称为![]() 的一个初等因子.
的一个初等因子.
[初等变换·矩阵的等价] 对λ矩阵![]() 的下列三种变换的有限次组合称为
的下列三种变换的有限次组合称为![]() 的初等变换.
的初等变换.
(i)任何两行(列)互换;
(ii)把任何一行(列)的各元素乘上同一个λ的多项式后加到另一行(列)的相应的元素上;
(iii)把任何一行(列)的元素乘上同一个不等于零的复数.
应当指出,适当地施行(ii),(iii)两种变换可以得到(i).
若![]() 可由
可由![]() 经过有限次初等变换得到,则称
经过有限次初等变换得到,则称![]() 与
与![]() 等价,记作
等价,记作![]() .
.
λ矩阵经过初等变换后,其不变因子和初等因子都不变.
[λ矩阵的标准形] 设λ矩阵![]() 的秩为r,不变因子为
的秩为r,不变因子为![]() ,则
,则
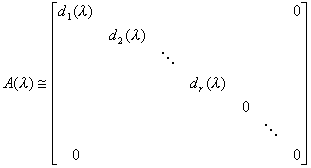
称右边的方阵为![]() 的标准形. 它是由
的标准形. 它是由![]() 唯一确定的.
唯一确定的.
等价的λ矩阵具有相同的标准形.
[特征矩阵] 方阵A的特征矩阵![]() 是一个特殊的λ矩阵. 所以
是一个特殊的λ矩阵. 所以
1o若![]() 的初等因子为
的初等因子为
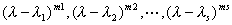
其中各![]() 未必两两不同,则
未必两两不同,则
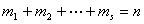
且有
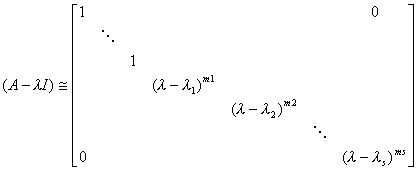
2o如果n阶λ矩阵
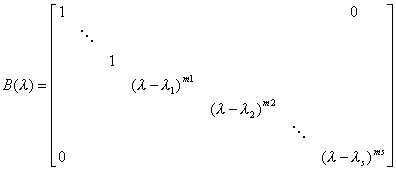
其中![]() ,则
,则
![]()
式中J为A的若当标准形.
3o若A的特征矩阵的初等因子为
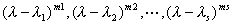
则
![]()
J为A的若当标准形.
[方阵标准化的步骤] 把方阵A化为A的若当标准形的步骤如下:
(1) 利用初等变换把![]() 化为对角矩阵,分解对角线上的多项式,就得到
化为对角矩阵,分解对角线上的多项式,就得到![]() 的全部初等因子.
的全部初等因子.
(2) 相应于每个初等因子![]() ,作出一个m阶的若当块
,作出一个m阶的若当块
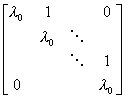
(3) 把全部若当块合并起来就得到A的若当标准形.
例1 求方阵
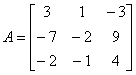
的若当标准形.
解
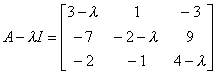
容易求出它的不变因子为1,1,![]() ,所以初等因子是
,所以初等因子是![]() ,因此得到A的若当标准形
,因此得到A的若当标准形

例2 求方阵
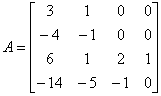
的若当标准形.
解
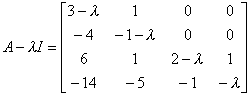
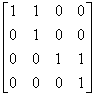
经过初等变换可以把它化为如下形式的对角线矩阵
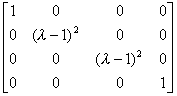
所以初等因子为![]() ,
,![]() ,相应的若当块为
,相应的若当块为
![]()
所以A的若当标准形为