2、解析开拓
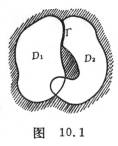
[直接解析开拓]如果
是两个有公共边界Г的单连通区域*，
和
分别在
和
内单值解析，在
Г和
Г上连续，并且在Г上
，那末称
是
经过Г向
内的直接解析开拓（或延拓）（图10.1）。
[解析开拓与完全解析函数]设
为单连通区域，
与
有公共边界
,
,对于任何k
,
在
内单值解析. 
与
分别在
和
上连续
,并且在
上
，那末称
是f1(z)经过一串区域向
内的解析开拓.
考虑f1(z)经过所有可能的区域串的各种解析开拓，把所有这些解析开拓的值当作一个函数F(z)的值来看。这时称F(z)为完全解析函数，而组成它的那些单值解析函数，即f1(z)的各种解析开拓，称为F(z)的分支.