3.解析函数的局部性质
[解析函数的零点]设![]() 在
在![]() 解析,并且
解析,并且![]() ,则称
,则称![]() 为
为![]() 的零点.若
的零点.若![]() 而
而![]() ,则称
,则称![]() 为
为![]() 的
的![]() 阶零点.
阶零点.
解析函数![]() 的零点是孤立的,也就是说,如果
的零点是孤立的,也就是说,如果![]() 是
是![]() 的零点,并且不是
的零点,并且不是![]() ,那末一定有一正数
,那末一定有一正数![]() ,使得
,使得![]() 在圆
在圆![]() 内除
内除![]() 外无其他零点.
外无其他零点.
[解析函数的唯一性定理] 设函数![]() 和
和![]() 在区域
在区域![]() 内解析,
内解析,![]() 的内点列
的内点列![]() (
(![]() )有一极限点
)有一极限点![]() 属于
属于![]() ,如果
,如果
,
那末在区域![]() 内
内
这个性质表明区域![]() 内的解析函数由
内的解析函数由![]() 内任一收敛于
内任一收敛于![]() 的内点的点列上的数值完全决定.
的内点的点列上的数值完全决定.
[孤立奇点(可去奇点·极点·本性奇点)] 如果函数![]() 在
在![]() 的一个邻域
的一个邻域![]() 内除
内除![]() 外解析,称
外解析,称![]() 是函数
是函数![]() 的一个孤立奇点.孤立奇点分三类:
的一个孤立奇点.孤立奇点分三类:
1o 当![]() (
(![]() 为有限数),
为有限数),![]() 称为
称为![]() 的可去奇点.
的可去奇点.![]() 是
是![]() 的可去奇点的充分必要条件是:
的可去奇点的充分必要条件是:![]() 在
在![]() 的邻域里*的罗朗级数不含主要部分,或者是
的邻域里*的罗朗级数不含主要部分,或者是![]() 在
在![]() 的邻域里有界.
的邻域里有界.
2o 当![]() ,
,![]() 称为
称为![]() 的极点.
的极点.![]() 是
是![]() 的极点的充分必要条件是:
的极点的充分必要条件是:![]() 在
在![]() 的邻域里的罗朗级数的主要部分只含有限多项,即
的邻域里的罗朗级数的主要部分只含有限多项,即
如果主要部分中![]() 的负次幂最高的是
的负次幂最高的是![]() ,那末称
,那末称![]() 为
为![]() 的
的![]() 阶极点.
阶极点.
3o 当![]() 不存在,
不存在,![]() 称为
称为![]() 的本性奇点.
的本性奇点.![]() 是函数
是函数![]() 的本性奇点的充分必要条件是:
的本性奇点的充分必要条件是:![]() 在
在![]() 的邻域里的罗朗级数中主要部分有无限多项.
的邻域里的罗朗级数中主要部分有无限多项.
如果![]() 是函数f(z)的本性奇点,那末对任意复数A,都存在一点列
是函数f(z)的本性奇点,那末对任意复数A,都存在一点列![]()
![]() ,
,![]() ,使得
,使得
[泰勒定理] 如果函数![]() 在区域
在区域![]() 内解析,那末对于
内解析,那末对于![]() 内一点
内一点![]() ,有
,有
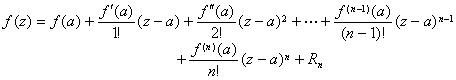
其中余项的形式是
C是以![]() 为圆心的圆周(
为圆心的圆周(![]() 的内部在
的内部在![]() 内).
内).
泰勒定理是讲解析函数的有限展开式,而泰勒级数展开定理(§4,一,1)是无穷级数形式.对于研究解析函数的局部性质来说,有用的还是这里的有限展开式.
[解析函数在无穷远点的性质]
1o 无穷远点的邻域以原点为中心,![]() 为半径的圆的外部所有的点是无穷远点的一个邻域.
为半径的圆的外部所有的点是无穷远点的一个邻域.
2o 无穷远点是![]() 的孤立奇点 设
的孤立奇点 设![]() .若
.若![]() 是
是![]() 的可去奇点,则称
的可去奇点,则称![]() 为
为![]() 的可去奇点;若
的可去奇点;若![]() 是
是![]() 的
的![]() 阶极点,则称
阶极点,则称![]() 为
为![]() 的
的![]() 阶极点;若
阶极点;若![]() 是
是![]() 的本性奇点,则称
的本性奇点,则称![]() 为
为![]() 的本性奇点.
的本性奇点.
3o 函数![]() 在无穷远点的罗朗级数 设
在无穷远点的罗朗级数 设![]() 在
在![]() 的邻域内的罗朗级数是
的邻域内的罗朗级数是
令![]() ,得到
,得到![]() 在
在![]() 的邻域内的罗朗级数
的邻域内的罗朗级数
,
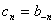
)
所以,当![]() 是
是![]() 的可去奇点时,
的可去奇点时,![]() 的罗朗级数中不含
的罗朗级数中不含![]() 的正次幂;当
的正次幂;当![]() 是
是![]() 的
的![]() 阶极点时,
阶极点时,![]() 的罗朗级数中,只有有限项
的罗朗级数中,只有有限项![]() 的正次幂,并且
的正次幂,并且![]() (
(![]() )是最后一个不等于零的系数;当
)是最后一个不等于零的系数;当![]() 是
是![]() 的本性奇点时,
的本性奇点时,![]() 的罗朗级数中,有无限多项
的罗朗级数中,有无限多项![]() 的正次幂.
的正次幂.
4o 函数![]() 在无穷远点是孤立奇点的性质 当
在无穷远点是孤立奇点的性质 当![]() 是
是![]() 的可去奇点时,函数的模在无穷远点的某一邻域里有界;当
的可去奇点时,函数的模在无穷远点的某一邻域里有界;当![]() 是
是![]() 的
的![]() 阶极点时,函数的模在无穷远点的任一邻域里无界;当
阶极点时,函数的模在无穷远点的任一邻域里无界;当![]() 是
是![]() 的本性奇点时,对任意复数
的本性奇点时,对任意复数![]() ,都存在点列
,都存在点列![]() ,
,![]() ,使得
,使得![]() .
.
5o 无穷远点是![]() 的零点
的零点 ![]() 的罗朗级数中不含
的罗朗级数中不含![]() 的正次幂,而且
的正次幂,而且![]() 。若
。若![]() ,而
,而![]() (
(![]() ),则称无穷远点是
),则称无穷远点是![]() 的
的![]() 阶零点.
阶零点.