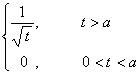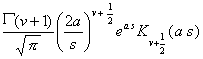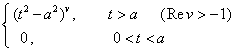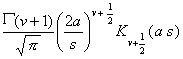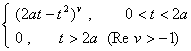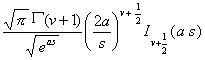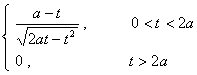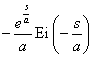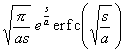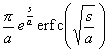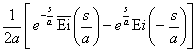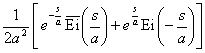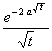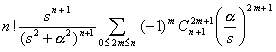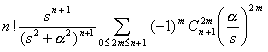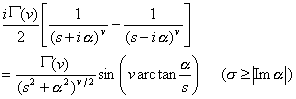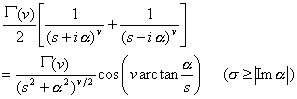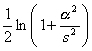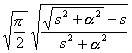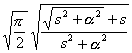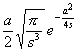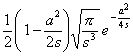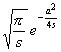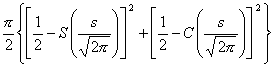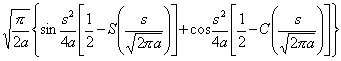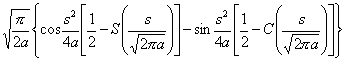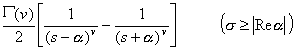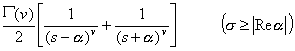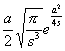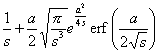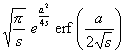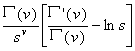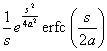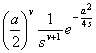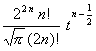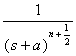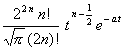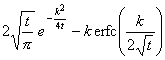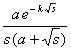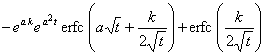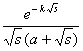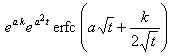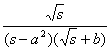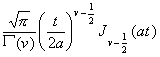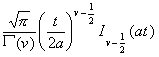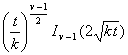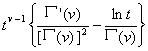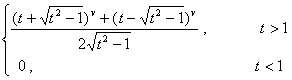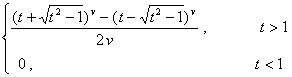§3 拉普拉斯变换
[拉普拉斯变换及其反演公式] ![]() 的拉普拉斯变换
的拉普拉斯变换
![]() (s是复数,s=
(s是复数,s=![]() )
)
拉普拉斯变换的反演公式
![]()
![]()
![]()
积分沿着任一直线Res=![]() 来取,
来取,![]() 是
是![]() 的增长指数,同时,积分理解为在主值意义下的.
的增长指数,同时,积分理解为在主值意义下的.
[拉普拉斯变换的存在条件] 如果![]() 满足下面三个条件,那末它的拉普拉斯变换存在.
满足下面三个条件,那末它的拉普拉斯变换存在.
(i)
实变量的复值函数![]() 和
和![]() 在
在![]() 上除掉有第一类间断点(在任一有限区间上至多有有限多个)外连续;
上除掉有第一类间断点(在任一有限区间上至多有有限多个)外连续;
(ii)
当t<0时,![]() =0;
=0;
(iii)
![]() 是有限阶的,也就是说可以找到常数
是有限阶的,也就是说可以找到常数![]() 和A>0,使得
和A>0,使得
![]()
![]()
这里数![]() 称为
称为![]() 的增长指数,
的增长指数,![]() 是有界函数时,可取
是有界函数时,可取![]() =0.
=0.
如果满足上面三个条件,那末L ( s )是半平面Res>![]() 上的解析函数.而反演公式在
上的解析函数.而反演公式在![]() 的连续点处成立.
的连续点处成立.
[拉普拉斯变换的性质]
![]() (a是常数)
(a是常数)
![]() (a,b是常数)
(a,b是常数)
![]()
式中
![]()
称为函数![]() 和g ( t
)的褶积(或卷积).
和g ( t
)的褶积(或卷积).
[拉普拉斯变换的主要公式表]
|
原 来 函 数 |
拉普拉斯变换后的函数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( n )( t ) |
|
|
|
|
|
|
|
|
原 来 函 数 |
拉普拉斯变换后的函数 |
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
f ( t2 ) |
|
|
t v-1f(t) (Rev
> |
|
|
|
|
|
|
L (ln s) |
|
|
|
|
|
|
|
|
|
|
|
|
[拉普拉斯变换表]
![]()
![]()
![]()
![]()
拉普拉斯变换表I
(已知函数查其拉普拉斯变换用此表方便)
|
f ( t ) |
L ( s ) |
|
|
1 |
|
|
e – c s |
|
1 |
|
|
t |
|
|
t n
|
|
|
|
|
|
t v
( Re v > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ea t |
|
|
tea t |
|
|
t nea t |
|
|
t vea t (
Re
v > |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
erf (at) ( a>0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
拉普拉斯变换表 II
(已知函数的拉普拉斯变换查其原来函数用此表方便)
|
L ( s ) |
f ( t ) |
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
|
|
[二重拉普拉斯变换及其反演公式]
函数f (x ,y)的二重拉普拉斯变换为
![]()
二重拉普拉斯变换的反演公式为
![]()
其中![]() .
.
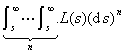
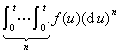
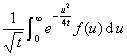
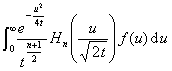
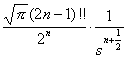
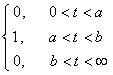
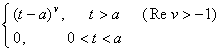
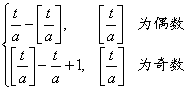 (a>0)
(a>0)