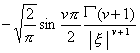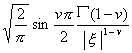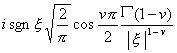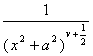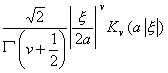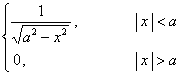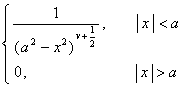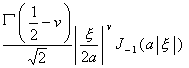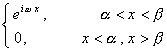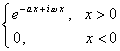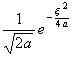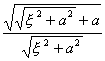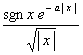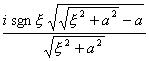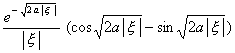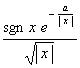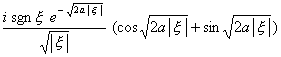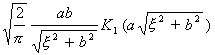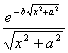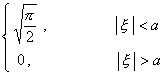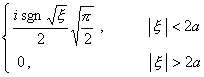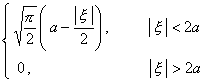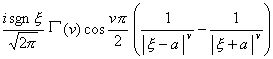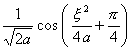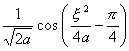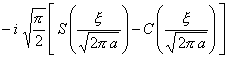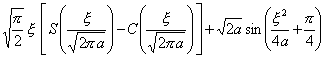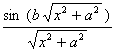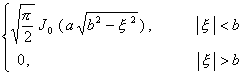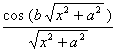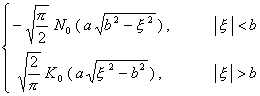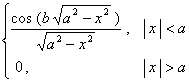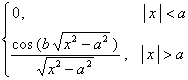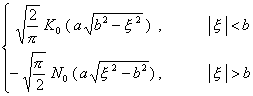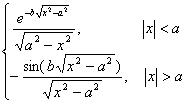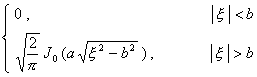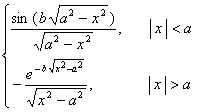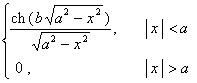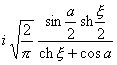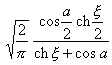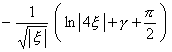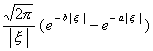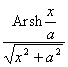二、 傅立叶变换
[傅立叶变换及其反演公式] ![]() 的傅立叶变换为
的傅立叶变换为
![]()
傅立叶变换的反演公式为
![]()
[傅立叶变换的存在条件] ![]() 的傅立叶变换及反演公式在满足下面两个条件下有意义(只是在
的傅立叶变换及反演公式在满足下面两个条件下有意义(只是在![]() 的间断点x0处,反演公式的左端应等于
的间断点x0处,反演公式的左端应等于![]() ):
):
1o ![]() 存在;
存在;
2o ![]() 在
在![]() 上满足狄利克莱条件:
上满足狄利克莱条件:![]() 只有有限个极值点,只有有限个第一类间断点.
只有有限个极值点,只有有限个第一类间断点.
[傅立叶变换的性质] 设![]() ,g
( x )的傅立叶变换分别是F(
,g
( x )的傅立叶变换分别是F(![]() ),G(
),G(![]() ),那末
),那末
1o 线性 a![]() +b
g ( x )的傅立叶变换是a F(
+b
g ( x )的傅立叶变换是a F(![]() )+b
G(
)+b
G(![]() )
(a,b是常数)
)
(a,b是常数)
2o 褶积(或卷积) f ( x )*g ( x )=![]() 的傅立叶变换是
的傅立叶变换是
F(![]() )
)![]() G(
G(![]() )
)
3o 帕塞法耳等式 ![]()
4o 翻转 f ( -x
)的傅立叶变换是F( -![]() ).
).
5 o 共轭 ![]() 的傅立叶变换是
的傅立叶变换是![]() .
.
6o 时移(延迟) f ( x-x0 )的傅立叶变换是![]() .
.
7o 频移(调频) ![]() 是
是![]() 的傅立叶变换 (
的傅立叶变换 (![]() 是常数).
是常数).
[傅立叶变换表]
![]() ,
, ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|