§3 线性微分方程
一、一般概念
[齐次线性微分方程与非齐次线性微分方程] 设微分方程
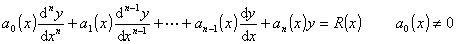 (1)
(1)如果方程中的未知函数![]() 及其各阶导数
及其各阶导数![]() 都是一次的,这种方程称为线性微分方程.因为
都是一次的,这种方程称为线性微分方程.因为![]() ,所以(1)称为n阶线性微分方程. 当
,所以(1)称为n阶线性微分方程. 当![]() ,(1)称为齐次线性微分方程.当
,(1)称为齐次线性微分方程.当![]() ,(1)称为非齐次线性微分方程.如果
,(1)称为非齐次线性微分方程.如果![]() 都是常数,(1)就称为常系数线性微分方程.
都是常数,(1)就称为常系数线性微分方程.
[解的存在和唯一性定理] 如果![]() 和
和![]() 在区间
在区间![]() 内连续,且
内连续,且![]() ,那末对任意给定的初始条件
,那末对任意给定的初始条件
![]()
方程(1)存在唯一解![]() ,式中
,式中![]() 为实数.
为实数.
[函数的线性相关性] 对于一组函数![]() ,如果有不全为零的常数
,如果有不全为零的常数![]() ,使等式
,使等式
![]()
在区间![]() 上成立,则称这组函数
上成立,则称这组函数![]() 在区间
在区间![]() 上线性相关.否则称这组函数线性无关(线性独立).
上线性相关.否则称这组函数线性无关(线性独立).
[朗斯基行列式] 如果![]() 是
是![]() 个
个![]() 次可微的函数,则称行列式
次可微的函数,则称行列式
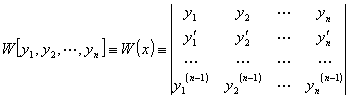
为函数![]() 的朗斯基行列式.
的朗斯基行列式.
朗斯基行列式具有以下性质:
1o 如果函数![]() 线性相关,那末它们的朗斯基行列式
线性相关,那末它们的朗斯基行列式
![]()
2o 如果函数![]() 是某齐次线性微分方程的解,那末它们线性相关的充分必要条件是它们的朗斯基行列式
是某齐次线性微分方程的解,那末它们线性相关的充分必要条件是它们的朗斯基行列式
![]()
[n阶齐次线性微分方程解的结构] 如果![]() 阶齐次线性微分方程
阶齐次线性微分方程
![]() ,
, ![]()
有![]() 个线性无关的解
个线性无关的解![]() .那末它的通解是这
.那末它的通解是这![]() 个解的线性组合,即
个解的线性组合,即
![]()
其中![]() 是任意常数.这时又称
是任意常数.这时又称![]() 为所给齐次线性微分方程的一组基本解.
为所给齐次线性微分方程的一组基本解.
[![]() 阶非齐次线性微分方程解的结构] 非齐次线性微分方程的通解是它的一个特解与对应齐次方程的通解之和,即
阶非齐次线性微分方程解的结构] 非齐次线性微分方程的通解是它的一个特解与对应齐次方程的通解之和,即
![]()
式中![]() 为任意常数.
为任意常数.