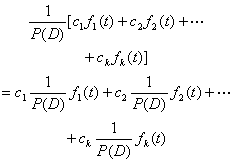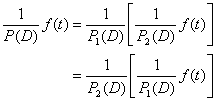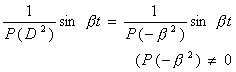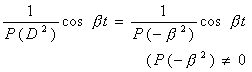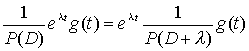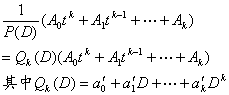四、   常系数非齐次线性微分方程的算子解法与方程组的算子解法（消去法）

    [微分算子与逆算子]  记

称D,D²,…,Dⁿ为微分算子.一般地引进微分算子（a₁,a₂,…,

a_n是常数）规定它的意义是

    还引进微分算子的逆算子，D^k的逆算子记为，规定它的意义是

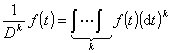       (k为正整数)

    P(D)的逆算子记为，它满足条件

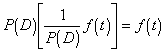
注意，的结果不是唯一的，而是一族函数.

    [微分算子的简单性质与运算公式]

微分算子	逆算子
1o  若c1，c2，…ck为常数，则      P(D)[c1f1(t)+ c2f2(t)+…           + ckfk(t)]    =c1P(D)f1(t)+ c2P(D)f2(t)+…           + ckP(D)fk(t)                      （线性） 2o  若P（D）= P1（D）·P2（D），则 P(D)f(t) = P1(D)[P2(D)f(t)]        = P2(D)[P1(D)f(t)]                      (交换律) 3o    P(D)eλt = eλtP(λ) 4o	若c1，c2，…ck为常数，则                                                            （线性） 若P（D）= P1（D）·P2（D），则   （交换律）                         (P(λ)≠0)
5o 6o  (位移定理) 7o	(位移定理) 设,则 按以下方法求得: 将P(D)(按D的升幂排列),依一般的多项式除法规则去除1,在第k+1步得到的商,当商中得到k次多项式时,除法停止,这k次多项式即Qk(D).

    上表中左栏各等式的意义是通常的，而右栏各等式的意义则是等号两边的函数族相同.

    [用算子解法求常系数非齐次线性微分方程的特解]

    1°  方程P(D)x=f_k(t)，其中f_k(t)是t的k次多项式.

    分两种情形：

    (i)  P(0)≠0.依上表公式7°得

    (ii)  P(0)=0.此时P(D)=Q(D)D^r（整数r≥1），而Q(0)≠0.依上表公式2°有

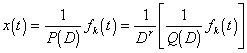
    设，则

    2°  方程（当f_k(t)为常数时P(λ)）.

依上表公式6° ，一个特解为

    3°  方程P(D)x=costf_k(t)或P(D)x=sintf_k(t).

    考虑辅助方程

    它与方程2°同类型，设它的一个特解是

那末方程                             

有一特解

x(t)=x₁(t)

而方程                         

有一特解

x(t)=x₂(t)

    4°  方程P(D²)x= 或P(D²)x=.

    若P()≠0，则由上表公式4°，5°得

或

    若P()=0,则有正整数r和多项式Q(Q()≠0)使

可按方程1° (ii)的方法处理.

    [用算子解法（消去法）求线性微分方程组的解]  消去法是解代数方程组的有效方法之一.引进微分算子之后，同样适用于解线性微分方程组.下面用具体例子来说明这个方法.

    设已给线性微分方程组

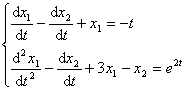
应用微分算子，上面方程组可写成

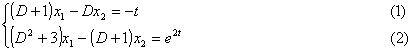
把这个方程组看成两个未知数x₁,x₂的代数方程组.利用消去法，依次解出x₁,x₂.

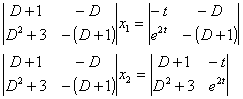
即

先解(1'),为此先求其对应的齐次方程

的通解.特征根为

λ₁=1,λ₂=i,λ₃=

所以齐次方程的通解为

     (为任意常数)

再用算子解法，求方程(1')的一个特解

由前表公式7°有

由前表公式3°有

得到方程(1')的特解

最后得出方程(1')的通解

为求出x₂ (t)，(1)减(2)得

用x₁(t)代入即得