§5 稳定性理论大意

    稳定性理论研究的是当微分方程右端函数与初始条件发生变化时，解的变化情况.

一、 稳定性的概念

    [解的稳定与不稳定]  设微分方程组

满足初始条件的解是.

    如果任意给定ε>0，总存在相应的正数δ=δ( t₀  ,ε)，使得只要初始值满足

此微分方程组相应的解 (i=1,2,…,n)对所有t>t₀就满足

则称解是稳定的.

    简单地说,如果初始值靠近某解初始值的所有解当t>t₀ 时总靠近某解,就说某解是稳定的.

    如果对于任意给定的ε>0，不管δ>0取得多么小，总存在满足

的初始值及τ>t₀，它相应的解不满足条件

则称解是不稳定的.

    如果稳定，并且初始值满足

的所有解都满足

则称是渐近稳定的.

    [问题的简化]  给定方程组

为了研究它满足初始条件的解的稳定性，必须考察别的解与它的偏差.今令

原方程组便变为如下形式：

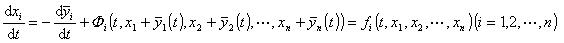       (1)

而的稳定性归结为方程组(1)的零解x_i≡0  (i=1,2,…,n) 的稳定性.

    任何微分方程组的常数解常称为它的平衡点（奇点）.所以(1)的零解

是平衡点.

    如果任意给定ε>0，总存在相应的正数δ=δ( t₀  ,ε)，使得只要初始值满足

(1)的相应解对所有t>t₀就满足

则称(1)的平衡点是稳定的.

如果进而满足条件

则称平衡点是渐进稳定的.

    如果不论正数δ选得多么小，对于预先给定的正数ε，总存在满足

的初始值及τ>t₀，它相应的解不满足条件

则称(1)的平衡点不稳定.

    [相空间]  给定方程组

称(x₁,x₂,…,x_n)的空间为此方程组的相空间，特别当n=2时，称为相平面.当方程组右端函数不显含t时，它的解作为相空间的曲线，称为轨道.在其他情况下，解曲线常称为积分曲线.