三、 边值问题
这里只讨论二阶线性常微分方程的边值问题.
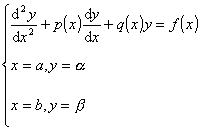(1) [差分方法] 将区间[a,b]分成n等份，步长
，分点x0=a, x1=a+h, …, xk=a+kh, …,xn=b 称为节点.把微商用差商代替，边值问题化为下面差分方程组的求解问题.
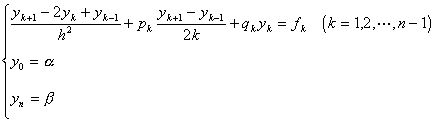
式中yk=y(xk),pk=p(xk),qk=q(xk),fk=f(xk) (
).上面的差分方程组可看成n+1个未知量y0,y1,y2,…,yn 的线性代数方程组，方程个数也是n+1.整理合并同类项，差分方程组可改写成
(
)
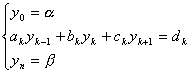式中
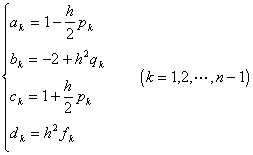
这是一种特殊形式的线性代数方程组,除了可用消元法，迭代法等求解外，还可用更简便有效的方法—追赶法(见第四章, §3).
在应用上，还可能遇到下面形式的边界条件：
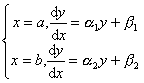
式中α1，α2，β1，β2是已知常数.这时，上面差分方程组中相应于边界条件的那两个方程要换成：
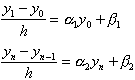
[化为初值问题的数值解] 先求出初值问题
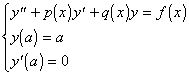
的数值解y0(x)，再求出满足初始条件y(a)=0,y'(a)=1的相应齐次方程
的数值解y1(x).原边值问题(1)的解可表示为
