§3  二阶偏微分方程

一、         二阶偏微分方程的分类、标准形式与特征方程

    考虑二阶偏微分方程

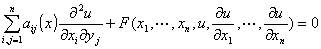                                       (1)

式中a_ij(x)=a_ij(x₁,x₂,…,x_n)为x₁,x₂,…,x_n的已知函数.

    [特征方程·特征方向·特征曲面·特征平面·特征锥面]

代数方程

称为二阶方程(1)的特征方程；这里a₁,a₂,…,a_n是某些参数，且有.如果点x°=(x₁°,x₂°,…,x_n°)满足特征方程，即

则过x°的平面的法线方向l:(a₁,a₂,…,a_n)称为二阶方程的特征方向；如果一个(n)维曲面，其每点的法线方向都是特征方向，则称此曲面为特征曲面；过一点的(n)维平面，如其法线方向为特征方向，则称这个平面为特征平面，在一点由特征平面的包络组成的锥面称为特征锥面.

    [n个自变量方程的分类与标准形式]  在点P(x₁°,x₂°,…,x_n°)，根据二次型

        (a_i为参量)

的特征根的符号，可将方程分为四类：

    (i)       特征根同号，都不为零，称方程在点P为椭圆型.

    (ii)    特征根都不为零，有n个具有同一种符号 ，余下一个符号相反，称方程在点P为双曲型.

    (iii)   特征根都不为零，有个具有同一种符号(n>m>1)，其余m个具有另一种符号，称方程在点P为超双曲型.

    (iv)     特征根至少有一个是零，称方程在点P为抛物型.

    若在区域D内每一点方程为椭圆型，双曲型或抛物型，则分别称方程在区域D内是椭圆型、双曲型或抛物型.

    在点P作自变量的线性变换可将方程化为标准形式：

    椭圆型：

    双曲型：

    超双曲型：

    抛物型：

式中Φ为不包含二阶导数的项.

    [两个自变量方程的分类与标准形式]  方程的一般形式为

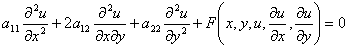                                (2)

 a₁₁,a₁₂,a₂₂为x,y的二次连续可微函数，不同时为零.

    方程

a₁₁dy²a₁₂dxdy+a₂₂dx²=0

称为方程(2)的特征方程.特征方程的积分曲线称为二阶方程(2)的特征曲线.

    在某点P(x₀,y₀)的邻域D内，根据Δ=a₁₂²－a₁₁a₁₂的符号将方程分类：

    当Δ>0时，方程为双曲型；

    当Δ=0时，方程为抛物型；

    当Δ<0时，方程为椭圆型.

在点P的邻域D内作变量替换，可将方程化为标准形式：

（i）       双曲型：因Δ>0，存在两族实特征曲线，，作变换，和方程化为标准形式

或                          

（ii）     抛物型: 因Δ=0，只存在一族实的特征曲线，取二次连续可微函数，使，作变换，，方程化为标准形式

（iii）    椭圆型：因Δ<0，不存在实特征曲线，设

为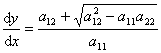的积分，不同时为零，作变量替换，,方程化为标准形式