3. 拉普拉斯方程
研究重力场、静力场、磁场以及一些物理现象(如振动、热传导、扩散)的平衡或稳定过程,通常得到椭圆型方程,最典型的方程为拉普拉斯方程
Δu=0
及泊松方程
Δu=ρ
式中ρ为已知函数,Δ为拉普拉斯算子,![]()
[圆或球的狄利克莱问题解的泊松积分] 当区域为圆或球时,分别采用极坐标(r,)或球坐标(r,θ,)较为方便.
Δu=0的极坐标形式为
![]()
Δu=0的球坐标形式为
![]()
狄利克莱问题解的泊松积分为
1°
区域是圆时,Δu=0, u|r=a=![]() ,解为泊松积分
,解为泊松积分
![]()
式中![]() 为已知连续函数,
为已知连续函数,![]() .
.
2°
区域是球时,Δu=0, u|r=a=![]() ,解为泊松积分
,解为泊松积分
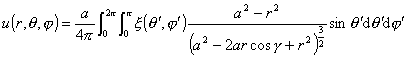
式中![]() 为已知连续函数,
为已知连续函数,
![]()
[调和函数的性质] 二维拉普拉斯方程的连续解称为调和函数,它具有以下重要性质:
1°
设函数u(x,y)在以S为边界的有界区域D内调和,在![]() 上有连续一阶偏导数,则
上有连续一阶偏导数,则
![]()
式中![]() 为外法向导数.
为外法向导数.
2° 算术平均值定理 设函数u(x,y)在圆的内部调和,在闭圆上连续,则u(x,y)在圆心的值等于它在圆周上的值的算术平均值.
3° 每一个调和函数u(x,y)对x,y无穷次可微.
4°
哈拉克第一定理(一致收敛定理)
设{uk(x,y)}, (k=1,2![]() )在有界区域D内调和,在
)在有界区域D内调和,在![]() 上连续,如果uk(x,y)在D的边界上一致收敛,则在D内也一致收敛,并且极限函数在D内调和.
上连续,如果uk(x,y)在D的边界上一致收敛,则在D内也一致收敛,并且极限函数在D内调和.
5° 哈拉克第二定理(单调性定理) 设调和函数列{uk(x,y)}, (k=1,2,…)在D的某一内点收敛,且对于任意k,
uk+1(x,y)≥uk(x,y)
则uk(x,y) 在D内处处收敛于某调和函数,同时在D的每一有界闭子区域上一致收敛.
6° 刘维尔定理 如函数u(x,y)在全平面上调和且不是常数,则它不可能有上界和下界.
7° 可去奇点定理 设u(x,y)在A点的一个邻域(除A点外)调和且有界,但在A点没有定义,则可定义函数u(x,y)在A点的值,使u在整个A点的邻域(包括A点)内是调和函数.
[李雅普诺夫闭曲面与内、外边值问题] 设S为En的有限闭曲面,如果满足下列条件,那末S称为李雅普诺夫闭曲面:
(i) 曲面到处有切面.
(ii) 存在常数d>0,对曲面上每一点P,可作一个以P为中心、d为半径的球,使曲面在此球内的部分和任意一条与P点法线平行的直线相交不多于一点
(iii) 曲面上任意二点P1及P2的法线的夹角γ(P1,P2)满足
![]()
式中A,δ为正常数,0<δ≤1,![]() 是点P1与P2之间的距离.
是点P1与P2之间的距离.
(iv) 从空间任意一点P0看曲面的任一部分σ的立体角有界,即
||≤k (k为常数)
(从点P0看曲面S的立体角为
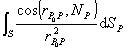
式中![]() 表示矢量
表示矢量![]() ,NP表示S在点P的外法线矢量,dSP表示点P的面积元素.)
,NP表示S在点P的外法线矢量,dSP表示点P的面积元素.)
设D为En的有界区域,其边界S为李雅普诺夫闭曲面.求在D内满足
Δu=0
而在S 上满足给定边界条件的解称为内边值问题;求在D外满足Δu=0而在S上满足给定边界条件的解称为外边值问题.
[狄利克莱问题与诺伊曼问题的解]
狄利克莱问题
Δu=0,![]()
诺伊曼问题
Δu=0,![]()
式中MS∈S,![]() 为S上的已知连续函数,
为S上的已知连续函数,![]() 为外法向导数.
为外法向导数.
1° 狄利克莱问题的解可表示为面积分
![]() .
.
式中v(P)称为面密度,面积分u(M)称为双层位势,rPM为点M与变点P之间的距离,rPM为矢量 ![]() ,NP为S在点P的外法线矢量,v(M)满足第二类弗雷德霍姆积分方程(第十五章§1):
,NP为S在点P的外法线矢量,v(M)满足第二类弗雷德霍姆积分方程(第十五章§1):
(i) 内边值问题
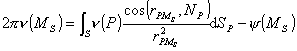
(ii) 外边值问题
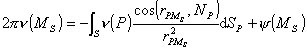
2° 诺伊曼问题的解可表示为面积分
![]()
式中(P)称为面密度,面积分u(M)称为单层位势,(P)满足第二类弗雷德霍姆积分方程:
(i) 内边值问题
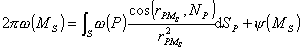
(ii) 外边值问题
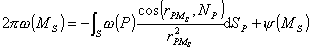
定理: 狄利克莱的内外边值问题及诺伊曼的外边值问题有惟一解,而诺伊曼的内边值问题解存在的充分必要条件是:
![]()
[泊松方程] 在区域D内,泊松方程Δu=ρ(ρ为已知连续函数)有特解:
三维: 体势位
![]()
二维: 对数势位
![]()
式中rPM为点M与变点P之间的距离.
如果已知泊松方程的一个特解U(M),则=u-U满足Δ=0,从而泊松方程的边值问题可化为拉普拉斯方程相应的边值问题.