3.  椭圆型方程的格林方法

    在区域D考虑椭圆型方程

式中a_ij,b_i,c,f为x₁,…,x_n的连续可微函数，a_ij=a_ji，二次型是正定的.

    [格林函数及其性质]  若Lu=0的共轭方程L*u=0的基本解G(x,)在D的边界S上满足

G(x,)=0,  x∈S

则称G(x,)为方程Lu=0的格林函数，式中x=(x₁,…,x_n)，ξ为参变点，=(₁,…,_n)，即G(x,)=G(x₁,…,x_n;

₁,…,_n).

    格林函数具有对称性质：设G(x,),V(x,)分别为方程Lu=0及其共轭方程的格林函数，则成立对称关系

G(x,)=V(x,)

特别如果Lu为自共轭微分算子，则有

G(x,)=G(,x)

    [利用格林函数解边值问题]

    1°  一般公式  在区域D上应用格林公式（本节，四），并取v=G(x,)，则方程Lu=f的狄利克莱问题u|_s=的解为

式中

      （N是S的外法线方向）

    2°  对于球体（球心为O，半径为a），u=0的基本解为，r为P(x,y,z)与参变点的距离，作M关于球面的反演点M₁，记r₁为M₁与P的距离，则格林函数为

.狄利克莱问题u|_s=的解为

式中S为球面.引用球坐标时，解为泊松积分(本节，三，3).

    3°  在圆上（半径为a），u=0的格林函数为

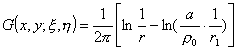
式中r为P(x,y)与参变点的距离，r₁为P与M点关于圆的反演点M₁的距离，圆上狄利克莱问题的解为泊松积分.