§4 偏微分方程的数值解法
一、 差分法
差分法是常用的一种数值解法.它是在微分方程中用差商代替偏导数,得到相应的差分方程,通过解差分方程得到微分方程解的近似值.
1. 网格与差商
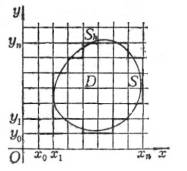
|
图14.7 |
在平面 (x , y)上的一以S为边界的有界区域D上考虑定解问题.为了用差分法求解,分别作平行于x轴和y轴的直线族.
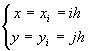 (i,
j=0,1,2,…,n)
(i,
j=0,1,2,…,n)
作成一个正方形网格,这里h为事先指定的正数,称为步长;网格的交点称为节点,简记为(i, j).取一些与边界S接近的网格节点,用它们连成折线![]() ,
,![]() 所围成的区域记作
所围成的区域记作![]() .称
.称![]() 内的节点为内节点,位于
内的节点为内节点,位于![]() 上的节点称为边界节点(图14.7).下面都在网格
上的节点称为边界节点(图14.7).下面都在网格![]() 上考虑问题:寻求各个节点上解的近似值.在边界节点上取与它最接近的边界点上的边值作为解的近似值,而在内节点上,用以下的差商代替偏导数:
上考虑问题:寻求各个节点上解的近似值.在边界节点上取与它最接近的边界点上的边值作为解的近似值,而在内节点上,用以下的差商代替偏导数:
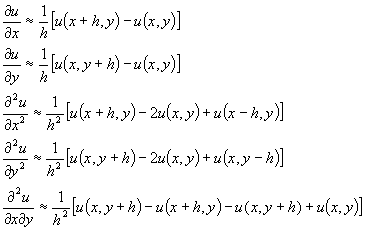
注意, 1° 式中的差商![]() 称为向后差商,而
称为向后差商,而![]() 称为向前差商,
称为向前差商,![]() 称为中心差商.也可用向前差商或中心差商代替一阶偏导数.
称为中心差商.也可用向前差商或中心差商代替一阶偏导数.
2° x轴与y轴也可分别采用不同的步长h, l,即用直线族
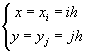 (i ,j=0, ±1, ±2
(i ,j=0, ±1, ±2![]() )
)
作一个矩形网格.