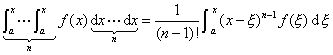2. 积分方程与微分方程之间的关系

某些积分方程可化为微分方程，也可从微分方程推导出积分方程。先来考虑二阶线性微分方程的初值问题：

                            （2）

若从方程(2)中解出，然后在区间(a,x)上对x求积分两次，利用初始条件，经过简单的计算不难得出*，

         

令

和

上式就可写为如下的形式:

                                                      (3)

这是一个第二类沃尔泰拉方程，核K是x的线性函数。

例1          初值问题

                                                        (4)

变为积分方程

                         (5)

反之，应用积分号下求导法则，微分两次就可把积分方程(3)化为微分方程(2)。在(3)及其第一次求导的结果中令x=a,就得给定初始条件。在例1中，对(5)式求导，得出

                           (6)

再求导一次得出原微分方程(4)，并从方程(6)和(5)给出初始条件

y(0)=1,  

对于边值问题，方法类似，先考虑一个简单的例子。

例2          从问题

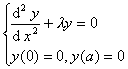
出发，积分两次，导出关系式

从此立刻可知条件y(0)=0成立。从第二端点条件y(a)=0决定C：

所以有关系式

                      (7)

令

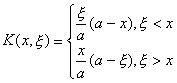
则方程(7)变为

                                                  (8)

这是第二类Fr方程。要从这个积分方程回到微分方程，只需对方程(8)求导两次，就得到

在积分方程(7)中，令x=0和x=a,可以直接推出边值条件y(0)=y(a)=0。

注意：在这个例中，

1°  在x=ξ处不连续，并当x增加而过ξ时有一跳跃-1。

2°  K是x的一个线性函数，即满足，且K 在端点x=0,x=a处等于零。

3°  K(x,ξ)=K(ξ,x),即核是对称的。

如果利用类似的方法，对更一般的具有齐次端点条件的二阶齐次方程的边值问题：

                      

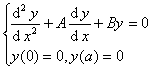
则除A=0外，可得在x=ξ不连续的一个核。