§5  非线性积分方程

[积分算子与线性算子]  考虑表达式

对于给定的核K(x,ξ),每个函数f(x)都有另一个函数F(x)与之对应，这种对应关系称为积分算子，记作K, 即

F=Kf

使得函数F=Kf存在的那些函数f的集合称为算子K的定义域。

    如果算子K满足条件

_{（a为常数）}

则称K为线性算子。

    [有界算子及其范数]  如果存在某常数M,对一切函数f都有

则称K为有界算子，式中表示函数f的范数(模)。使上面不等式成立的一切M的最大下界称为算子K的范数，记作，它也可以定义为

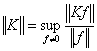
    有界算子具有以下性质：

    1°  若K₁和K₂是有界算子，则K₁K₂也是有界算子。

    2°  如果对有限正方形k₀(a≤x≤b, a≤ξ≤b)上的一切x,ξ,函数K(x,ξ)是连续的，则由

定义的算子K 是有界算子。

    3°  如果在无限区间[a,b]上，函数K(x,ξ)满足

则由

定义的算子K是有界算子。

[非线性积分方程解的存在定理]  考虑如下形式的积分方程

                                             (1)

前几节中解线性积分方程的方法对于非线性积分方程是不适用的。下面仅列出几个解的存在性定理。

    定理1  假定K(x,ξ)对单位正方形k₀(0≤x≤1,0≤ξ≤1)上的一切x,ξ是连续的，设ôK(x,ξ)ô≤C ⁽C为常数⁾，对单位正方形k₀上的一切ξ, t也是连续的，并且

        (A为常数)

又假定满足李普希茨条件

式中B是与ξ无关的常数。那末当时，积分方程(1)在L₂[0,1]^*中有唯一的解。

    定理2  假定K(x,ξ)对单位正方形k₀上的一切x,ξ是连续的，设

            （C为常数）

满足

             （B为常数）

并对任意ε>0，都有δ=δ(ε)使得

     （当时）

式中。那么当时，积分方程(1)在L₂[0,1]*中至少有一个解。

    定理3  假定K(x,ξ)和都是它们的自变量的连续函数，设S是L₂[0,1]中满足

   （M为常数）

的函数的全体。假定

  （C为常数）

（一切）

并对任意ε>0，都存在δ=δ(ε),使得

     （当时）

那末当时，积分方程(1)在S中至少有一个解。

    这个定理的条件要求K(x,ξ)是连续的，事实上可以证明，只要核K(x,ξ)是平方可积的就有同样的结论。

    定理4  假定满足定理3所述的条件，并设K(x,ξ)满足

                         

那末当时，积分方程(1)在S中至少有一个解。